A Versatile Discrete Simulator
Table of Contents
- 1. What are we talking about?
- 2. Representing spike trains
- 2.1. The "problem"
- 2.2. Exercise: Memory size of a large bit array in
Python - 2.3. Exercise: Storing spike trains on disk, how and when?
- 2.4. Exercise: Keeping a dynamic window on the past
- 2.5. Solution: Memory size of a large bit array in
Python - 2.6. Solution: Storing spike trains on disk, how and when?
- 2.7. Solution: Keeping a dynamic window on the past
- 3. Representing the model
- 3.1. Introduction
- 3.2. Exercise: Step one, coding the leakage functions \(g_{i \to j}(\,)\)
- 3.3. Exercise: Step two, dealing with unavoidable function calls \(\phi_i(\,)\)
- 3.4. Exercise: Step three, neuron class
- 3.5. Exercise: Step four, synaptic graph representation
- 3.6. Exercise: Step five, neuronal dynamics representation
- 3.7. Exercise: Step six, Network class
- 3.8. Solution: Step one, coding the leakage functions \(g_{i \to j}(\,)\)
- 3.9. Solution: Step two, dealing with unavoidable function calls \(\phi_i(\,)\)
- 3.10. Solution: Step three, neuron class
- 3.11. Solution: Step four, synaptic graph representation
- 3.12. Solution: Step five, neuronal dynamics representation
- 3.13. Solution: Step six, Network class
1. What are we talking about?
1.1. A Directed graph
Chapter 2 introduces successively two "flavors" of a discrete time model. The basic ingredients of the model are:
- a finite set \(I\) of \(n\) neurons \(N_i\), \(i \in I \equiv \{1,\ldots,n\}\),
- a family of synaptic weights \(w_{j \to i} \in \mathbb{R}\), for \(j, i \in I\),
- a family of spiking probability functions \(\phi_i : \mathbb{R} \to [0, 1 ] , i \in I\).
We introduce: \[ {\mathcal V}_{ \cdot \to i } = \{ j \in I : w_{j \to i } \neq 0\} ,\] the set of presynaptic neurons of \(i\), and \[ {\mathcal V}_{ i \to \cdot } = \{ j \in I : w_{i \to j } \neq 0\} ,\] the set of postsynaptic neurons of \(i\). We observe that this defines a graph in which the neurons are the vertices and the synaptic connections are the edges. Since synaptic connections are generally not symmetrical, we are dealing with directed graphs. For the illustrations we are going to consider \(w_{i\rightarrow j} = 0\) or \(1\) and we can then view these weights as the elements of the graph adjacency matrix.
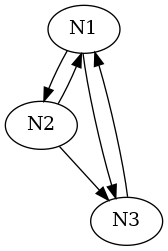
1.1.1. Example
For a case with 3 neurons: N1, N2 and N3, where N1 has N2 and N3 as postsynaptic partners, both with weights 1; N2 has N1 and N3 as postsynaptic partners, both with weights 1; and N3 has N1 has postsynaptic partner with weight 1, the adjacency matrix is:
| . | 1 | 1 |
| 1 | . | 1 |
| 1 | . | . |
where we write "." instead of "0" following a convention commonly used for sparse matrix representations. The \(\mathcal{V}_{\cdot \rightarrow i}\) are then the columns of the adjacency matrix, while the \(\mathcal{V}_{i \rightarrow \cdot}\) are its rows. We will also use graphical representations for these matrices as illustrated here:
We can and will generalize the construction of the adjacency matrix by using elements that are not necessarily 0 (no connection) or 1 (connection) but by plugging-in the actual \(w_{i\rightarrow j}\) values.
1.2. Basic discrete time model
In the discrete time setting, our model describes the spiking activity of a finite set \(I\) of neurons over time, where time is binned into small windows of length around \(1\) to \(5\) milliseconds. For any neuron \(i \in I\), \(X_t (i ) = 1\) indicates the presence of a spike within the time window of index \(t\), and \(X_t (i ) = 0\) indicates the absence of a spike within the same time window. In what follows, we will simply speak of the value at time \(t\) instead of speaking of the time window of index \(t\).
In the following table, which can be viewed as simplified raster plot, the top row contains the time index. Each subsequent row contains a snapshot of the realizations of 3 processes. The notation \(x(i)\) (\(i=1,2,3\)) should be understood as: \[ x(i) \equiv \left(\ldots,x_{-2}(i),x_{-1}(i),x_{0}(i),x_{1}(i),x_{2}(i),x_{3}(i),x_{4}(i),x_{5}(i),\ldots\right)\,.\] To describe the model, we also need to introduce the notion of the last spike time of neuron i before time t, for any \(i \in I\) and \(t \in \mathbb{Z}\). Formally, this is defined by
\begin{equation}\label{eq:L_t-discrete-definition} L_t (i) = \max \{ s \le t : X_s (i) = 1 \} . \end{equation}1.2.1. Example: raster plot
In the table, the right columns shows the realization \(l_5(i)\) of \(L_5(i)\) for each of the three processes.
| t | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … | \(l_{5}(\,)\) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x(1) | … | . | 1 | . | . | 1 | . | . | 1 | … | \(l_{5}(1)=5\) |
| x(2) | … | 1 | . | 1 | . | . | . | . | . | … | \(l_{5}(2)=0\) |
| x(3) | … | 1 | . | . | . | . | 1 | . | . | … | \(l_{5}(3)=3\) |
Here, 1 is used to indicate the last spike.
1.3. Membrane potential: a very simple model
The membrane potential of neuron \(i\) at time \(t\) is defined
\begin{equation}\label{def:potential} V_t (i) = \left\{\begin{array}{lr} \sum_{j \in I} w_{ j \to i} \left( \sum_{ s = L_t (i) +1 }^{ t}X_s (j) \right) , & \text{ if } L_t (i ) < t \\ 0, & \text{ if } L_t (i ) = t \end{array} \right. \end{equation}Thus, the membrane potential value is of neuron \(i\) obtained by adding up the contributions of all presynaptic neurons \(j \in {\mathcal V}_{\cdot \to i }\) of i since its last spiking time. The membrane potential is moreover reset to \(0\) at each spiking time of the neuron. With such a scheme, a neuron cannot interact with itself—more precisely there is no difference between a model where \(w_{i \to 1} = 0\) and a model where \(w_{i \to 1} \neq 0\).
1.3.1. Example: membrane potential trajectories
Using the previous adjacency matrix, the above realizations lead to:
| t | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
|---|---|---|---|---|---|---|---|---|---|---|
| v(1) | … | ? | 0 | 1 | 1 | 0 | 1 | 1 | 0 | … |
| v(2) | … | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 2 | … |
| v(3) | … | 0 | 1 | 2 | 2 | 2 | 0 | 0 | 1 | … |
We see that \(v_{-2}(1)\) is not defined ("?") since \(l_{-2}(1)\) is missing.
1.4. Dynamics: what makes a neuron spike?
We start with an informal description of the dynamics assuming that we have reached time \(t\):
- We compute \(V_t(i)\) for every neuron \(i\).
- Every neuron \(i\) decides to spike at time \(t+1\) with probability \(\phi_i ( V_t (i ) )\), independently of the others: \(\mathbb{P}\{X_{t+1} (i ) = 1 \mid V_t(i)\} = \phi_i ( V_t (i ) )\).
- For every neuron \(i\), we compute \(V_{t+1} (i)\) according to \eqref{def:potential}.
This algorithm can be formally translated as follows.
- We start at time \(t=0\) from some initial condition \(X_t (i ) = x_t (i )\) for all \(t \le 0, i \in I\).
- We suppose that for all \(i \in I\), there exist \(\ell_i \le 0\), such that \(x_{\ell_i} (i ) = 1\). This means that \(\ell_i \le L_0 (i) \le 0\) is well-defined for any \(i \in I\), and that we are able to compute \(V_0 ( i)\) for each neuron \(i\). We call such a past configuration an admissible past.
- We consider a family of uniform random variables \(U_t (i ) , i \in I, t \geq 1\), which are independent and identically distributed (IID), with a uniform distribution on \([0, 1 ]\) (\(U_t(i) \sim \mathcal{U}(0,1)\)).
Then we define in a recursive way for every \(t \geq 0\):
\begin{equation}\label{def:fixedpast} X_{t+1 } (i )=\left\lbrace \begin{array}{ll} 1 , & \mbox{if } U_{t+1} ( i) \le \phi_i (V_{t }(i ) ) \\ 0 , & \mbox{if } U_{t+1} ( i) > \phi_i ( V_{t }(i ) ) \end{array}, \right. \end{equation}where for each \(t\geq 1\) and \(i\in I\), \(V_{t}( i )\) is the membrane potential of neuron \(i\) at the previous time step \(t\), defined according to (\ref{def:potential}).
It is easy to show (and its done in the book) that the process \((\mathbb{V}_t)_{t \geq 0 }\), \(\mathbb{V}_t =( V_t (i),i \in I)\), is a Markov chain on \(\mathbb{R}^n\) and therefore more suitable for simulations. We can see \(\mathbb{V}_{t}\) as a vector valued random variable:
\begin{equation}\label{eq:bigV} \mathbb{V}_{t} \equiv \begin{bmatrix} V_t(1) \\ V_t(2) \\ \vdots \\ V_t(n) \end{bmatrix} \end{equation}The transitions of the Markov chain \((\mathbb{V}_{t})_{t} \geq 0\) can be described as follows:
\begin{equation}\label{eq:simple-discrete-V-evolution} V_{t+1 } (i )=\left\lbrace \begin{array}{ll} 0 , & \mbox{if } U_{t+1} ( i) \le \phi_i (V_{t }(i ) ) \\ V_{t} (i ) + \sum_{j \in I } w_{ j\to i } \mathbb{1}_{ \{ U_{t+1} ( j) \le \phi_j (V_{t }(j ) \}} , & \mbox{if } U_{t+1} ( i) > \phi_i ( V_{t }(i ) ) . \end{array} \right. \end{equation}In other words, \[V_{t+1} (i ) = ( 1 - X_{t+1}(i) ) \left[ V_t (i ) + \sum_{j \in I } w_{j \to i } X_{t+1} (j ) \right].\]
1.5. Extending the model considered in the book
For modeling purpose we are likely to be willing to include two features of actual neuron dynamics:
- a refractory period: after a spike a neuron cannot immediately spike again. That period is of a variable length depending on the neuron's type and is usually in the 1 to 10 ms range. This refractory period is mainly due to a combination of sodium channels inactivation and, more importantly, to a large potassium conductance that: i) clamps the membrane potential to the potassium reversal potential, slightly below the "resting potential" (our null potential here), see Chap. 1 of the book; ii) shunts most of the incoming synaptic inputs.
- a synaptic delay: a synapse gets activated once the action potential reaches it, this means that the action potential has to travel from the soma to the synapse along the axon and this is not instantaneous (as in the above model), but depends on the axon length (one of the actual geometric properties that are ignored by our "point" neuron model as discussed in Chap. 1 of the book). Then, once the action potential reaches the synapse, there is an essentially fixed delay of 1 to 2 ms to complete the synaptic transmission.
The model we have so far discussed implicitly assumes that both the refractory period and the synaptic delay are taken care of in a single time step. We could nevertheless meet modeling settings were realist considerations (our co-author A. Galves, following the 19th Century french authors, would rather use the term naturalist than realist) lead us to include explicit refractory periods or synaptic delays. We therefore discuss now how we could (slightly) extend our framework.
1.5.1. Including an explicit refractory period
This is very "simply" done, we associate to each neuron \(i \in I\) a refractory period \(r_i \in \{1,2,...,r_{\text{max}}\}\) and we replace \eqref{def:potential} by:
\begin{equation}\label{def:potential-with-rp} V_t (i) = \left\{\begin{array}{ll} \sum_{j \in I} w_{ j \to i} \left( \sum_{ s = L_t (i) + \textcolor{red}{r_i} }^{ t}X_s (j) \right) &, \text{ if } L_t (i ) < t \\ 0 &, \text{ if } L_t (i ) = t \end{array} \right. \end{equation}then \eqref{def:potential} is a special case of \eqref{def:potential-with-rp} where \(r_i = 1\), \(\forall i \in I\). If we take \(r_i = 2\) for \(i \in \{1,2,3\}\) in Ex. 1.3.1, we get (modified entries appear in red):
| t | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
|---|---|---|---|---|---|---|---|---|---|---|
| v(1) | … | ? | 0 | \(\textcolor{red}{0}\) | 1 | 0 | \(\textcolor{red}{0}\) | 1 | 0 | … |
| v(2) | … | 0 | \(\textcolor{red}{0}\) | 0 | 0 | \(\textcolor{red}{0}\) | 1 | 1 | \(\textcolor{red}{1}\) | … |
| v(3) | … | 0 | \(\textcolor{red}{0}\) | \(\textcolor{red}{1}\) | 2 | 2 | 0 | 0 | \(\textcolor{red}{0}\) | … |
The inclusion of a "non trivial" refractctory period (\(r_i > 1\)) in Eq. \eqref{def:potential-with-rp} breaks the Markov property enjoyed by the process \((\mathbb{V}_t)_{t \geq 0 }\) whose dynamics is defined by Eq. \eqref{eq:simple-discrete-V-evolution}. An equivalent of the latter should indeed be written:
\begin{equation}\label{eq:discrete-V-evolution-with-rp} V_{t+1 } (i )=\left\lbrace \begin{array}{ll} 0 , & \mbox{if } U_{t+1} ( i) \le \phi_i (V_{t }(i ) ) \\ V_{t} (i ) + \sum_{j \in I } w_{ j\to i } \textcolor{red}{\mathbb{1}_{\{t+1 \ge L_t(i)+r_i\}}} \, \mathbb{1}_{ \{ U_{t+1} ( j) \le \phi_j (V_{t }(j ) \}} , & \mbox{if } U_{t+1} ( i) > \phi_i ( V_{t }(i ) ) . \end{array} \right. \end{equation}We see here that \(V_{t+1}(i)\) depends expicitely on \(L_t(i)\). This means that we must make our state space larger to make room for \(L_t(i)\), namely \((\mathbb{R}^n \times \mathbb{Z}^n)\), in order to get back the Markov property (we need potentially negative values of \(L_t(i)\) to initialize our process, that is why we have \(\mathbb{Z}^n\) and not \(\{0,1,\ldots\}^n\) here). We then have to consider the joint processes: \(\left(\mathbb{V}_t,\mathbb{L}_t\right)_{t \geq 0 }\), where the transitions of \(\mathbb{V}_t\) are given by Eq. \eqref{eq:discrete-V-evolution-with-rp} and the transition of \(\mathbb{L}_t\) are given by:
\begin{equation}\label{eq:discrete-L-evolution} L_{t+1}(i) = \mathbb{1}_{\{U_{t+1} ( i) \le \phi_i (V_{t }(i ) )\}} \, (t+1) + \, \mathbb{1}_{\{U_{t+1} ( i) > \phi_i (V_{t }(i ) )\}} \, L_t(i)\, . \end{equation}We can see \(\mathbb{L}_t\) as a vector valued random variable:
\begin{equation}\label{eq:bigL} \mathbb{L}_{t} \equiv \begin{bmatrix} L_t(1) \\ L_t(2) \\ \vdots \\ L_t(n) \end{bmatrix} \end{equation}1.5.2. Including an explicit synaptic delay
This is also "simply" done by adding to each pair \((j,i)\) for which \(w_{j \to i} \neq 0\) a delay \(\tau_{j \to i} \in \{0,1,2,\ldots, \tau_{max}\}\), with \(\tau_{max} < \infty\). Eq. \eqref{def:potential-with-rp} becomes:
\begin{equation}\label{def:potential-with-rp-and-delay} V_t (i) = \left\{\begin{array}{ll} \sum_{j \in I} w_{ j \to i} \left( \sum_{ s = L_t (i) + r_i }^{ t}X_{s\textcolor{red}{- \tau_{j\to i}}}(j) \right), & \text{ if } L_t (i ) < t\\ 0, & \text{ if } L_t (i ) = t \end{array} \right. \end{equation}If \(r_i = 1\), \(\forall i \in I\), Eq. \eqref{eq:simple-discrete-V-evolution} becomes:
\begin{equation}\label{eq:complex-discrete-V-evolution} V_{t+1 } (i )=\left\lbrace \begin{array}{ll} 0, & \mbox{if } U_{t+1} ( i) \le \phi_i (V_{t }(i ) ) \\ V_{t} (i ) + \sum_{j \in I } w_{ j\to i } \mathbb{1}_{ \{ U_{t+1\textcolor{red}{- \tau_{j\to i}}} ( j) \le \phi_j (V_{t\textcolor{red}{- \tau_{j\to i}} }(j ) \}}, & \mbox{if } U_{t+1} ( i) > \phi_i ( V_{t }(i ) ) . \end{array} \right. \end{equation}We see that \(V_{t+1 } (i )\) does not depend only on \(\left(V_{t } (1 ), V_{t } (2),\ldots, V_{t } (n )\right)\) anymore, but that we have to go back in time to \(\tau_{max}\). So the nice Markov property we had seems to be lost again.
If we are in the general case, we can consider the joint processes: \[(\mathbb{S}_t)_{t \ge 0} \equiv \left(\mathbb{V}_t,\mathbb{L}_t, \mathbb{X}_t\right)_{t \geq 0 }\, ,\] on the state space \(\mathbb{R}^n \times \mathbb{Z}^n \times \{0,1\}^{n \times (\tau_{max}+1)}\), where \(\mathbb{X}_t\) is defined by:
\begin{equation}\label{eq:bigX} \mathbb{X}_{t} \equiv \begin{bmatrix} X_{t-\tau_{max}}(1) & X_{t-\tau_{max}+1}(1) & \cdots & X_{t}(1) \\ X_{t-\tau_{max}}(2) & X_{t-\tau_{max}+1}(2) & \cdots & X_{t}(2) \\ \vdots & \vdots & \ddots & \vdots \\ X_{t-\tau_{max}}(n) & X_{t-\tau_{max}+1}(n) & \cdots & X_{t}(n) \end{bmatrix} \end{equation}\(\mathbb{X}_{t}\) is just the subset of all the past events (spike or no spike) generated by the network that can still influence what will happen at \(t+1\).
Then Eq. \eqref{eq:discrete-V-evolution-with-rp} and \eqref{eq:discrete-L-evolution} can be generalized as follows:
\begin{align} V_{t+1 } (i ) &= \mathbb{1}_{\{U_{t+1} ( i) > \phi_i (V_{t }(i ) )\}} \, \left(V_{t} (i ) + \mathbb{1}_{\{t+1 \ge L_t(i) + r_i\}} \, \left(\sum_{j \in I } w_{ j\to i } X_{t-\tau_{j \to i}+1}(j)\right) \right)\, , \label{eq:discrete-V-at-t+1-given}\\ L_{t+1 } (i ) &= \mathbb{1}_{\{U_{t+1} ( i) \le \phi_i (V_{t }(i ) )\}} \, (t+1) + \, \mathbb{1}_{\{U_{t+1} ( i) > \phi_i (V_{t }(i ) )\}} \, L_t(i)\, , \label{eq:discrete-L-at-t+1-given} \\ X_{t+1 } (i ) &= \mathbb{1}_{\{U_{t+1} ( i) \le \phi_i (V_{t }(i ) )\}} \, . \label{eq:discrete-X-at-t+1-given} \end{align}We then recover the Markov property.
Notice that the introduction of potentially non-null synaptic delays makes the introduction of self-interaction (\(w_{i \to i} \neq 0\)) meaningful if \(\tau_{i \to i} > r_i\). This can be used to favor a weakly periodic discharge. Imagine for instance that:
- \(\phi_i(v) = \max(0,\min(1,v))\); in other words, \(\phi_i(\,)\) is linear with slope 1 between 0 and 1, is null below 0 and 1 above 1;
- \(r_i = 5\);
- \(w_{i \to i} = 0.7\).
Let us assume that \(i\) spiked at \(t=0\) and that \(i\) is isolated (\(\mathcal{V}_{\cdot{} \to i} = \emptyset\)). Then:
- \(\mathbb{P}\{X_t(i) = 1 \mid L_t(i) \le 5\} = 0\) (refractory period effect);
- \(\mathbb{P}\{X_t(i) = 1 \mid L_t(i) > 5\} = 0.7\).
The probability for observing the next spike at:
- \(t=6\) is 0.7;
- \(t=7\) is \(0.3 \times 0.7\);
- \(t=8\) is \(0.3^2 \times 0.7\);
- …
The distribution of the inter spike interval is therefore a shifted geometric distribution (the shift is 5 and the parameter of the distribution is 0.7). This implies that we have a 0.99 probability for observing the next spike between \(t=6\) and \(t=10\).
1.6. Membrane potential: introducing leakage
The membrane of a neuron is not a perfect insulator and the synaptic inputs have finite duration meaning that the membrane potential deviations tends towards zero in the absence of input. We take this fact into account by adding to the above dynamics (using the symbol \(\mathbb{Z}_{0+}\) for \(\{0,1,2,\ldots\}\), the non negative integers)
a family of leak functions \(g_{j \to i} : \mathbb{Z}_{0+} \to \mathbb{R}_+ , i,j \in I\).
Every function \(g_{j \to i}\) describes how an input from neuron \(j\) to neuron \(i\) loses its effect due to leakage over time. Introducing leakage in the model, the membrane potential of neuron \(i\) at time \(t\) is now given by
\begin{equation}\label{def:potentialwithg} V_t (i) = \left\{\begin{array}{lr} \sum_{j \in I} w_{ j \to i} \left( \sum_{ s = L_t (i) + r_i }^{ t} g_{j \to i} (t-s) X_{s- \tau_{j\to i}}(j) \right) , & \text{ if } L_t (i ) < t \\ 0, & \text{ if } L_t (i ) = t \end{array} \right. \end{equation}Then Eq. \eqref{eq:discrete-V-at-t+1-given} must be replaced by:
\begin{equation}\label{eq:discrete-V-at-t+1-given-with-leak} V_{t+1 } (i ) = \mathbb{1}_{\{U_{t+1} ( i) > \phi_i (V_{t }(i ) )\}} \, \times \left(\sum_{j \in I } w_{ j\to i } \left( \sum_{ s = L_{t} (i) + r_i }^{ t+1} g_{j \to i} (t+1-s) X_{s- \tau_{j\to i}}(j) \right)\right)\, . \end{equation}Notice that when \(\mathbb{1}_{\{U_{t+1} ( i) > \phi_i (V_{t }(i ) )\}} = 1\), \(L_{t+1}(i) = L_t(i)\) (Eq. \eqref{eq:discrete-L-at-t+1-given}), this is why the inner summation starts from \(s = L_{t} (i) + r_i\). Notice also that in the general case where the \(g_{j \to i}\) could have unbounded supports, the Markov property is lost since \(L_t(i)\) can also be infinitely far in the past.
1.6.1. A simple setting with leakage
If, for all \(i,j \in I\), \(g_{j \to i} ( s) = \rho_i^s\) for all \(s \geq 0\), for some \(\rho_i \in [0,1]\); if \(r_i=1\) and \(\tau_{j \to i} = 0\); then \((\mathbb{V}_t)_{t \geq 0 }\) is a Markov chain whose transitions are given by:
\begin{equation}\label{eq:leaky-discrete-V-evolution} V_{t+1}(i)=\left\{ \begin{array}{lr} 0 & : U_{t+1}(i) \le \phi_i (V_{t}(i )) \\ \rho_i V_{t}(i) + \sum_{j \in I } w_{ j\to i } \mathbb{1}_{\{ U_{t+1}(j) \le \phi_j (V_{t }(j)) \}} & : U_{t+1}(i) > \phi_i (V_{t}(i )) \end{array} \right. \end{equation}1.6.2. Leakage with compact support
When we will simulate models with leakage that do not correspond to the geometric case of the previous section, we will only consider leakage functions with finite (compact) support. That is, there will be a \(t_{max} < \infty\) such that \(g_{j \to i} (t) = 0\), \(\forall t \ge t_{max}\). Our leakage functions can then be fully specified by vectors in \(\mathbb{R}^{t_{max}}\):
\begin{equation}\label{eq:leakage-with-finite-support} g_{j \to i} (\,) = \left(g_{j \to i}(0), g_{j \to i}(1),\ldots, g_{j \to i}(t_{max}-1)\right) \, . \end{equation}The Markov property is then recovered on the state space: \(\mathbb{R}^n \times \mathbb{Z}^n \times \{0,1\}^{n \times (\tau_{max}+\textcolor{red}{t_{max}}+1)}\) with the process: \((\mathbb{S}_t)_{t \ge 0} \equiv \left(\mathbb{V}_t,\mathbb{L}_t, \mathbb{X}_t\right)_{t \geq 0 }\) where \(\mathbb{X}_t\) is now a bigger matrix than in Eq. \eqref{eq:bigX} since it has to go further back in the past:
\begin{equation}\label{eq:bigbigX} \mathbb{X}_{t} \equiv \begin{bmatrix} X_{t-\tau_{max}\textcolor{red}{-t_{max}}}(1) & X_{t-\tau_{max}\textcolor{red}{-t_{max}}+1}(1) & \cdots & X_{t}(1) \\ X_{t-\tau_{max}\textcolor{red}{-t_{max}}}(2) & X_{t-\tau_{max}\textcolor{red}{-t_{max}}+1}(2) & \cdots & X_{t}(2) \\ \vdots & \vdots & \ddots & \vdots \\ X_{t-\tau_{max}\textcolor{red}{-t_{max}}}(n) & X_{t-\tau_{max}\textcolor{red}{-t_{max}}+1}(n) & \cdots & X_{t}(n) \end{bmatrix} \end{equation}1.7. What do we want?
We want a program able to simulate the Markov chains defined by equations \eqref{eq:discrete-V-at-t+1-given} or \eqref{eq:discrete-V-at-t+1-given-with-leak}, \eqref{eq:discrete-L-at-t+1-given} and \eqref{eq:discrete-X-at-t+1-given}.
2. Representing spike trains
2.1. The "problem"
We are going to simulate spike trains in discrete time, that is, objects that are usually pictured (and even stored) as bit arrays as we did in Sec. 1.2.1. We should therefore pause and ask ourselves what is the best, or at least a reasonable, way to store such objects in the computer's memory knowing that there are two basic constraints to satisfy:
- a "small" memory footprint,
- a fast access (more precisely we want to know quickly if there was a spike at an arbitrary time in the past).
We will therefore try out different solutions in the following exercises. Our testing scenario will be a Bernoulli process: our \(X_t(i)\) are IID with \(\mathbb{P}\{X_t(i) = 1\} = \rho\), \(0 \le \rho \le 1\). The actual value of \(\rho\) should play a big role. To fix ideas we will consider a train defined on \(2^{20}\) time steps (because 20 is the smallest integer, \(i\), such that \(2^i \ge 10^6\)) where we could think of the actual (physical) value of a time step to be 1 ms (the fastest spiking neurons are found in the cochlea and spike at 1 kHz, for us; they can spike at higher rates in bats). With a 1 ms time step and a maximal discharge rate of 1 kHz, there is at most one spike (per neuron) per time step. Then \(2^{20}\) time steps correspond to roughly 17.5 minutes in real time.
2.2. Exercise: Memory size of a large bit array in Python
You are going to use function getsizeof from the sys module of the standard library to measure the memory size of your objects. Your "reference" bit array, ref_lst, is generated as follows:
from random import seed, random import sys seed(20061001) rho = 0.01 ref_lst = [random() <= rho for i in range(2**20)] sys.getsizeof(ref_lst)
8448728
We can see that this size corresponds very closely to \(2^{20}\) pointers in a 64 bits (8 bytes) addressable space:
sys.getsizeof(ref_lst)/8/2**20
1.007166862487793
This is because a list in Python is an array of pointers and getsizeof returns the memory taken by this array of pointers only; it does not include the (memory) size of the objects pointed to—see Chap. 5 of Goodrich, Tamassia and Goldwasser, Data Structures and Algorithm in Python (2013)—. It is possible to call recursively getsizeof using a code available on GitHub in the recipe-577504-compute-mem-footprint repository, this code by Raymond Hettinger is distributed under an MIT license and a copy of it is located in our code/mem_footprint.py of this repository.
So, if we call function total_size on our ref_list we get:
from code.mem_footprint import total_size print(total_size(ref_lst,verbose=True))
8448728 <class 'list'> [False, False, False, False, False, False, ...] 24 <class 'bool'> False 28 <class 'bool'> True 8448780
Here, we see that the list takes 8448728 Bytes as we had before, the elements (pointers) of this list point to only two kinds of eleemnts, False (that takes 24 Bytes) and True (that takes 28 Bytes), leading to a total size of: 8448728 + 24 + 28 = 8448780 Bytes.
Answer the following:
- What is the expected value of
sum(ref_lst), what is its variance, is what we got compatible with these values (use a standard score)? - Simulate a list,
idx_lstthat contains the indices of the elements ofref_lstthat are 1. Check that youridx_lstlist contains the same events asref_lst. Compare the memory size ofidx_lstwith the one ofref_lst. - Use method
arrayfrom the array module of the standard library to make an array version ofref_lstusingunsigned charencoding and an array version ofidx_lstusingunsigned intencoding (on my machine it is enough since 4 Bytes are used per element which is more than the 2 Bytes that are guaranteed; so you might have to useunsigned long). Compare the memomry sizes with the one ofref_lst. - Store
ref_lstin a numpy array with Boolean elements (specify your data type). Make a memory size comparison. - Use a
numpypackbits array to storeref_lst. Make a size comparison. Whenpackbitsarray are used, the element of the latter are unsigned integers coded with 8 bit (1 Byte). Writing \(r_0,r_1,\ldots,r_7\) the first 8 elements ofref_lst, the first element of the packed array is: \(\sum_{i=0}^7 r_i \times 2^{7-i}\). - Write a one line command that returns if a spike was present at time \(0 \le t \le 2^{20}-1\) from the
packbitsversion of the spike train obtained in the previous question. Test it with the first spike timeidx_lst[0]and at the previous time (idx_lst[0]-1). - Repeat some of the above comparisons with a "success probability", \(\rho\) equal to 0.1, then 0.5.
2.3. Exercise: Storing spike trains on disk, how and when?
We consider the same general framework as in the previous exercises set 2.2 adding to it a more realistic element: a network. We now want to simulate \(n=10^3\) neurons for \(10^6\) time steps. Storing all the data in RAM with a numpy array and a Boolean data type (that takes 1 Byte per element) would require \(10^3 \times 10^6 = 10^9 = 1 GByte\). We might then consider the option of writing the data to disk as the simulation proceeds. More precisely, we are going to explore the extra cost of writing to disk, after each time step, the indices of the neurons that spiked in a text format. The key issue is execution time, measured with the functions provided by the timeit module of the standard library. The file size is of secondary importance, since we can always compress it if necessarily. We start by writing a function that takes the success probability, rho, and the network size, ntw_size, as argument and that returns a function (more precisely a closure) implementing a single time step of the simulation: it draws/selects each neuron with a probability rho:
def mk_sgl_step_iid(rho, ntw_size): """Returns a closure generating a single step by IID draws of 'ntw_size' neurons with probability 'rho'. Parameters ---------- rho: a real between 0 and 1 ntw_size: a positive integer Returns ------- A function that returns a list whose elements are integers between 0 and 'ntw_size'-1, the list might be empty. """ if not (0 < rho < 1): raise ValueError("Expecting: 0 < rho < 1") if not isinstance(ntw_size,int): raise TypeError("ntw_size should be an integer.") if not ntw_size > 0: raise ValueError("Expecting: ntw_size > 0.") def sgl_step_iid(): from random import random return [i for i in range(ntw_size) if random() <= rho] return sgl_step_iid
We can then check how long it takes to call a function returned by mk_sgl_step_iid(0.01,1000) \(2^{20}\) times (without writing anything to disk):
import timeit from random import seed sgl_step_iid = mk_sgl_step_iid(0.01,1000) seed(20110928) print(timeit.timeit('for i in range(2**20): sgl_step_iid()', number=1, globals=globals()))
64.73117658798583
Notice that this code spends a lot of time allocating space in memory since every call to sgl_step_iid generates a new list.
Q.1 Modify the above code such that it writes to disk the indices at which the list returned by each call to sgl_step_iid() is True and time it (it is easier to write a function that does the job and to time the latter).
Using numpy random sub-module and a different strategy, we could try to limit memory allocation with:
def mk_sgl_step_iid_np(rho, ntw_size, seed): """Returns a closure generating a single step by IID draws of 'ntw_size' neurons with probability 'rho'. Parameters ---------- rho: a real between 0 and 1 ntw_size: a positive integer seed: the seed of the PRNG Returns ------- A function that returns a list whose elements are integers between 0 and 'ntw_size'-1, the list might be empty. """ import numpy as np if not (0 < rho < 1): raise ValueError("Expecting: 0 < rho < 1") if not isinstance(ntw_size,int): raise TypeError("ntw_size should be an integer.") if not ntw_size > 0: raise ValueError("Expecting: ntw_size > 0.") state = np.zeros(ntw_size, dtype=np.float64) idx = np.arange(ntw_size) rng = np.random.default_rng(seed) def sgl_step_iid_np(): rng.random(out=state) return list(idx[state <= rho]) return sgl_step_iid_np
We can then check how long it takes to call a function returned by mk_sgl_step_iid_np(0.01,1000,20061001) \(10^6\) times (without writing anything to disk):
sgl_step_iid_np = mk_sgl_step_iid_np(0.01,1000,20061001) print(timeit.timeit('for i in range(2**20): sgl_step_iid_np()', number=1, globals=globals()))
12.399544308020268
Q.2 Modify the above code such that it writes to disk the indices at which the list returned by each call to sgl_step_iid_np() is True and time it (it is easier to write a function that does the job and to time the latter).
2.4. Exercise: Keeping a dynamic window on the past
In the most general form of our model, Sec. 1.6, part of the past network activity is included in the specification of the system's state: Eq. \eqref{eq:bigX} and \eqref{eq:leaky-discrete-V-evolution}. We could of course keep the whole network past activity, but as argued in the previous exercise, this could become a very large object to keep in RAM. If we decide to keep only the most recent (up to \(\tau_{max}\) in the past) activity we have to find an efficient way to perform the following operation at the end of each time step:
\begin{equation}\label{eq:bigXdyn} \begin{bmatrix} X_{t-\tau_{max}}(1) & X_{t-\tau_{max}+1}(1) & \cdots & X_{t}(1) \\ X_{t-\tau_{max}}(2) & X_{t-\tau_{max}+1}(2) & \cdots & X_{t}(2) \\ \vdots & \vdots & \ddots & \vdots \\ X_{t-\tau_{max}}(n) & X_{t-\tau_{max}+1}(n) & \cdots & X_{t}(n) \end{bmatrix} \to \begin{bmatrix} X_{t-\tau_{max}+1}(1) & X_{t-\tau_{max}+2}(1) & \cdots & X_{t+1}(1) \\ X_{t-\tau_{max}+1}(2) & X_{t-\tau_{max}+2}(2) & \cdots & X_{t+1}(2) \\ \vdots & \vdots & \ddots & \vdots \\ X_{t-\tau_{max}+1}(n) & X_{t-\tau_{max}+2}(n) & \cdots & X_{t+1}(n) \end{bmatrix} \end{equation}In other words, we go from \(\mathbb{X}_t\) to \(\mathbb{X}_{t+1}\) by removing the first column of \(\mathbb{X}_t\), moving all the remaining columns to the left and putting \(\left(X_{t+1}(i)\right)_{i\in I}\) as the rightmost column. We also have to keep in mind that this \(\mathbb{X}_t\) is stored in memory because we will often need to query it, that is answer question like: was \(X_{t-12}(5) = 1\). What we really need is a good compromise between a fast implementation of Eq. \eqref{eq:bigXdyn} and a fast query. We will focus on a single row of \(\mathbb{X}_t\) since in our "real" simulation code this matrix will be accessed by rows. We have to decide if we use the binary array representation: all the \(X_{u}(i)\) are stored for \(u \in \{t-\tau_{max},\ldots,t\}\) regardless of their realization (0 or 1); or if only the indices in \(u\) at which \(X_u(i) = 1\). Notice that the storage issue that concerned us in Sec. 2.2 is not that important here since \(\tau_{max}\) is typically "small" compared to the number of time steps of the simulation (we are talking of something of the order of 10 against something of the order of \(10^6\)). The first strategy works with a fixed length container (list or array), while the second works with a variable length one. This is important to consider since memory allocation/de-allocation (required by the second approach) is potentially costly. We will consider three strategies that we now describe.
2.4.1. A linked list
A linked list or something close to it, is a uni-dimensional container to which we can add new items to the right (when \(\mathbb{1}_{U_{t+1}(i) \le \phi_i\left(V_t(i)\right)} = 1\)) and from which we can remove an item from the left (\(t-\tau_{max}\) was in the list and we advanced by one time step). This is directly provided by a Python list, the first operation is implemented by the append method and the second by the pop method, as illustrated by the following example:
from random import seed, random seed(20061001) tau_max = 5 rho = 0.25 lst = [] t = 0 while t < 20: if random() <= rho: lst.append(t) print("Event at time: " + str(t)) if len(lst) > 0 and lst[0] < t-tau_max: lst.pop(0) print("List at time " + str(t) +": " + str(lst)) t += 1
List at time 0: [] List at time 1: [] List at time 2: [] List at time 3: [] Event at time: 4 List at time 4: [4] List at time 5: [4] List at time 6: [4] List at time 7: [4] List at time 8: [4] List at time 9: [4] List at time 10: [] Event at time: 11 List at time 11: [11] Event at time: 12 List at time 12: [11, 12] List at time 13: [11, 12] List at time 14: [11, 12] List at time 15: [11, 12] Event at time: 16 List at time 16: [11, 12, 16] Event at time: 17 List at time 17: [12, 16, 17] List at time 18: [16, 17] List at time 19: [16, 17]
Clearly, a linked list of fixed length can also be used:
from random import seed, random seed(20061001) tau_max = 5 rho = 0.25 lst = [0]*(tau_max+1) t = 0 while t < 20: lst.pop(0) if random() <= rho: lst.append(1) print("Event at time: " + str(t)) else: lst.append(0) print("List at time " + str(t) +": " + str(lst)) t += 1
List at time 0: [0, 0, 0, 0, 0, 0] List at time 1: [0, 0, 0, 0, 0, 0] List at time 2: [0, 0, 0, 0, 0, 0] List at time 3: [0, 0, 0, 0, 0, 0] Event at time: 4 List at time 4: [0, 0, 0, 0, 0, 1] List at time 5: [0, 0, 0, 0, 1, 0] List at time 6: [0, 0, 0, 1, 0, 0] List at time 7: [0, 0, 1, 0, 0, 0] List at time 8: [0, 1, 0, 0, 0, 0] List at time 9: [1, 0, 0, 0, 0, 0] List at time 10: [0, 0, 0, 0, 0, 0] Event at time: 11 List at time 11: [0, 0, 0, 0, 0, 1] Event at time: 12 List at time 12: [0, 0, 0, 0, 1, 1] List at time 13: [0, 0, 0, 1, 1, 0] List at time 14: [0, 0, 1, 1, 0, 0] List at time 15: [0, 1, 1, 0, 0, 0] Event at time: 16 List at time 16: [1, 1, 0, 0, 0, 1] Event at time: 17 List at time 17: [1, 0, 0, 0, 1, 1] List at time 18: [0, 0, 0, 1, 1, 0] List at time 19: [0, 0, 1, 1, 0, 0]
2.4.2. A fixed length linked-list based on an array
The array object of the array module also provide the necessary methods append and pop needed to reproduce the last exemple, so lets try:
from array import array from random import seed, random seed(20061001) tau_max = 5 rho = 0.25 lst = array('B',[0]*(tau_max+1)) t = 0 while t < 20: lst.pop(0) if random() <= rho: lst.append(1) print("Event at time: " + str(t)) else: lst.append(0) print("List at time " + str(t) +": " + str(list(lst))) t += 1
List at time 0: [0, 0, 0, 0, 0, 0] List at time 1: [0, 0, 0, 0, 0, 0] List at time 2: [0, 0, 0, 0, 0, 0] List at time 3: [0, 0, 0, 0, 0, 0] Event at time: 4 List at time 4: [0, 0, 0, 0, 0, 1] List at time 5: [0, 0, 0, 0, 1, 0] List at time 6: [0, 0, 0, 1, 0, 0] List at time 7: [0, 0, 1, 0, 0, 0] List at time 8: [0, 1, 0, 0, 0, 0] List at time 9: [1, 0, 0, 0, 0, 0] List at time 10: [0, 0, 0, 0, 0, 0] Event at time: 11 List at time 11: [0, 0, 0, 0, 0, 1] Event at time: 12 List at time 12: [0, 0, 0, 0, 1, 1] List at time 13: [0, 0, 0, 1, 1, 0] List at time 14: [0, 0, 1, 1, 0, 0] List at time 15: [0, 1, 1, 0, 0, 0] Event at time: 16 List at time 16: [1, 1, 0, 0, 0, 1] Event at time: 17 List at time 17: [1, 0, 0, 0, 1, 1] List at time 18: [0, 0, 0, 1, 1, 0] List at time 19: [0, 0, 1, 1, 0, 0]
2.4.3. A circular buffer
We can choose to work with a fixed length list on which we implement a circular buffer as shown on stackoverflow that we modify as follows.
class circularlist(object): from array import array def __init__(self, size): """Initialization""" self.index = 0 self.size = size self._data = array('B',[0]*size) def append(self, value): """Append an element""" self._data[self.index] = value self.index = (self.index + 1) % self.size def __getitem__(self, key): """Get element by index, relative to the current index""" return(self._data[(key + self.index) % self.size]) def __repr__(self): """Return string representation""" return str([self[i] for i in range(self.size)])
With this class defined, the previous example becomes:
from random import seed, random seed(20061001) tau_max = 5 rho = 0.25 buffer = circularlist(tau_max+1) t = 0 while t < 20: if random() <= rho: print("Event at time: " + str(t)) buffer.append(1) else: buffer.append(0) print("Buffer at time " + str(t) +": " + str(buffer)) t += 1
Buffer at time 0: [0, 0, 0, 0, 0, 0] Buffer at time 1: [0, 0, 0, 0, 0, 0] Buffer at time 2: [0, 0, 0, 0, 0, 0] Buffer at time 3: [0, 0, 0, 0, 0, 0] Event at time: 4 Buffer at time 4: [0, 0, 0, 0, 0, 1] Buffer at time 5: [0, 0, 0, 0, 1, 0] Buffer at time 6: [0, 0, 0, 1, 0, 0] Buffer at time 7: [0, 0, 1, 0, 0, 0] Buffer at time 8: [0, 1, 0, 0, 0, 0] Buffer at time 9: [1, 0, 0, 0, 0, 0] Buffer at time 10: [0, 0, 0, 0, 0, 0] Event at time: 11 Buffer at time 11: [0, 0, 0, 0, 0, 1] Event at time: 12 Buffer at time 12: [0, 0, 0, 0, 1, 1] Buffer at time 13: [0, 0, 0, 1, 1, 0] Buffer at time 14: [0, 0, 1, 1, 0, 0] Buffer at time 15: [0, 1, 1, 0, 0, 0] Event at time: 16 Buffer at time 16: [1, 1, 0, 0, 0, 1] Event at time: 17 Buffer at time 17: [1, 0, 0, 0, 1, 1] Buffer at time 18: [0, 0, 0, 1, 1, 0] Buffer at time 19: [0, 0, 1, 1, 0, 0]
2.4.4. Binary encoding
We consider here a genuine binary coding of the rows of \(\mathbf{x}_t\), a realisation of \(\mathbb{X}_t\). More precisely, the above example at time 17 with a \(\tau_{max} = 5\) corresponds to:
\[\left(x_{12}(i)=1, x_{13}(i)=0, x_{14}(i)=0, x_{15}(i)=0, x_{16}(i)=1, x_{17}(i)=1\right)\]
We can represent the binary sequence 100011 by the integer 35:
\[35 = 1 \times 2^5 + 0 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0\, ,\] in Python the conversion is automatically performed by prefixing the sequence with "0b":
x_17 = 0b100011
x_17
35
From this point, advancing by one time step is simply done by multiplying the number by 2 (a left shift 35 << 1) before taking the modulus with \(2^6\):
x_18 = (x_17 << 1) % 2**6 print("{0:0>6b}".format(x_18))
000110
If a spike occurs, we just have to add 1. Then when we write:
t = 17 seq = 0b110001 seq <<= 1 seq %= 2**6 seq += 1 print("Sequence at time {0:2d} : {1:0>6b}".format(t,seq))
Sequence at time 17 : 100011
the sequence "100011" should be read from right to left. Time is 17 and the rightmost element is 1, so there was a spike at time 17. The second rightmost element is 1, so there was also a spike at time 17-1=16, the next three rightmost elements are 0, so there were no spike at times 17-2=15, 17-3=14 or 17-4=13; the leftmost element is 1, so there was a spike at time 17-5=12.
In order to know quickly if there was a spike s time step before t (s=0,1,2,3,4,5) we can simply use a binary left shift >> operation with t-s steps and check if the remainder of a division by 2 is 1:
t = 17 print("The present time is " + str(t)) print("Was there a spike at time " + str(t) + "?") print(" " + str((x_17 >> (t-t)) % 2 == 1)) print("Was there a spike at time " + str(t-1)+ "?") print(" " + str((x_17 >> (t-t+1)) % 2 == 1)) print("Was there a spike at time " + str(t-2)+ "?") print(" " + str((x_17 >> (t-t+2)) % 2 == 1))
The present time is 17 Was there a spike at time 17? True Was there a spike at time 16? True Was there a spike at time 15? False
So let us re-code our previous example:
from random import seed, random seed(20061001) tau_max = 5 nb_seq = 2**(tau_max+1) rho = 0.25 seq = 0b0 t = 0 while t < 20: seq <<= 1 seq %= nb_seq if random() <= rho: seq += 1 print("Event at time : " + str(t)) print("Sequence at time {0:2d} : {1:0>6b}".format(t,seq)) t += 1
Sequence at time 0 : 000000 Sequence at time 1 : 000000 Sequence at time 2 : 000000 Sequence at time 3 : 000000 Event at time : 4 Sequence at time 4 : 000001 Sequence at time 5 : 000010 Sequence at time 6 : 000100 Sequence at time 7 : 001000 Sequence at time 8 : 010000 Sequence at time 9 : 100000 Sequence at time 10 : 000000 Event at time : 11 Sequence at time 11 : 000001 Event at time : 12 Sequence at time 12 : 000011 Sequence at time 13 : 000110 Sequence at time 14 : 001100 Sequence at time 15 : 011000 Event at time : 16 Sequence at time 16 : 110001 Event at time : 17 Sequence at time 17 : 100011 Sequence at time 18 : 000110 Sequence at time 19 : 001100
We can try doing the same thing using the numpy types and functions:
import numpy as np rng = np.random.default_rng(20061001) tau_max = 5 nb_seq = 2**(tau_max+1) rho = np.float64(0.25) seq = np.uint8(0) n_past = np.uint8(2**(tau_max+1)-1) one = np.uint8(1) t = 0 while t < 20: seq = np.left_shift(seq,one) seq = np.bitwise_and(seq,n_past) if rng.random() <= rho: seq += 1 print("Event at time : " + str(t)) print("Sequence at time {0:2d} : {1:0>6b}".format(t,seq)) t += 1
Sequence at time 0 : 000000 Event at time : 1 Sequence at time 1 : 000001 Sequence at time 2 : 000010 Sequence at time 3 : 000100 Event at time : 4 Sequence at time 4 : 001001 Sequence at time 5 : 010010 Event at time : 6 Sequence at time 6 : 100101 Event at time : 7 Sequence at time 7 : 001011 Sequence at time 8 : 010110 Sequence at time 9 : 101100 Event at time : 10 Sequence at time 10 : 011001 Sequence at time 11 : 110010 Sequence at time 12 : 100100 Sequence at time 13 : 001000 Sequence at time 14 : 010000 Sequence at time 15 : 100000 Sequence at time 16 : 000000 Sequence at time 17 : 000000 Sequence at time 18 : 000000 Sequence at time 19 : 000000
2.4.5. Question
Take \(\tau_{max} = 50\), \(2^{20}\) steps, a success probability of 0.01 (making IID draws as usual). Initialize your "past" as an empty list when using a variable length scheme (first case of Sec. 2.4.1) or with zeros for a fixed length scheme. At each time step draw a result, make the "past" evolve and draws to integers, j and k, uniformly from \(\{0,1,\ldots, \tau_{max}\}\), before checking if the past contains a spike at time \(t-j\) and \(t-k\). Consider all the above schemes as alternatives (always starting from the same seed) and use timeit to compare them. As an example for the fixed length linked list described in Sec. 2.4.1, you should write something like:
def sim_with_fixed_length_linked_list(n_steps=2**20, rho_success=0.01, tau_max=50): from random import random, randint past = [0]*(tau_max+1) t = 0 found_in_past = 0 while t < n_steps: past.pop(0) if random() <= rho_success: past.append(1) else: past.append(0) j = randint(0,tau_max) found_in_past += past[tau_max-j] k = randint(0,tau_max) found_in_past += past[tau_max-k] t += 1 print("Found: " + str(found_in_past)) return found_in_past import timeit from random import seed seed(20061001) print(timeit.timeit('sim_with_fixed_length_linked_list()', number=10, globals=globals()))
Found: 20773 Found: 21312 Found: 21316 Found: 20974 Found: 21268 Found: 21059 Found: 20887 Found: 20812 Found: 21493 Found: 20955 18.371022567007458
The code prints the number of spike founds while exploring the past (this is done twice after each time step, making an expected value for this number of \(2 \times 0.01 \times 2^{20} = 20971.52\)). This is a way to (partially) check that the different implementations do generate exactly the same sequences (as long as they start from the same seed).
2.5. Solution: Memory size of a large bit array in Python
2.5.1. Q.1
We are considering here \(2^{20}\) IID draws from a binomial distribution with a parameter of 0.01, we therefore expect:
2**20*0.01
10485.76
successes with a variance of:
2**20*0.01*(1-0.01)
10380.9024
The z-score is:
from math import sqrt (sum(ref_lst) - 2**20*0.01)/sqrt(2**20*0.01*(1-0.01))
-0.7141264788892625
Our simulation is compatible with a draw from a Binomial distribution with \(n=2^{20}\) and \(p=0.01\).
2.5.2. Q.2
We simulate idx_lst as follows:
from random import seed, random import sys seed(20061001) idx_lst = [i for i in range(2**20) if random() <= 0.01] print(total_size(idx_lst))
376740
We compare the contents with:
all([ref_lst[i] for i in idx_lst])
True
The size comparison with getsizeof:
sys.getsizeof(ref_lst)/sys.getsizeof(idx_lst)
99.19141542218465
This ratio is what we expect considering that only a fraction of 0.01 elements of ref_lst are equal to 1. Therefore, the memory size of idx_lst is very close to the size of an array of pointers (with an 8 bytes addressable space) with len(idx_lst) elements:
sys.getsizeof(idx_lst)/(8*len(idx_lst))
1.0224719101123596
If we compare the real sizes we get:
total_size(ref_lst)/total_size(idx_lst)
22.42602325211021
The ratio is smaller because the objects to which the elements of the idx_lst list are pointing to are all different integers leading to a real memory size of: len(idx_lst) * (8+28) since the memory taken by an integer in Python (at least on my machine) is 28 Bytes. 28 Bytes is really a lot for an integer; it is propbably because there is no size limit for integers in Python.
2.5.3. Q.3
We store ref_lst in an array of array with an unsigned char encoding:
from array import array ref_array = array('B',ref_lst) total_size(ref_array)
1048656
This is indeed what we expect from \(2^{20}\) elements taking 1 Byte each. The ratio with our reference is:
total_size(ref_lst)/total_size(ref_array)
8.056769808211653
Again that makes sense: every element of ref_lst is a pointer (taking 8 Bytes) to one of 2 immutable objects (True or False), while every element of ref_array takes 1 Byte.
We now store idx_lst in an array of array with an unsigned int encoding:
idx_array = array('I',idx_lst) total_size(idx_array)
41732
The ratio with our reference is:
total_size(ref_lst)/total_size(idx_array)
202.45327326751652
That's getting huge!
2.5.4. Q.4
We store ref_lst in a Boolean numpy array with:
import numpy as np ref_np = np.array(ref_lst,dtype=np.bool_) total_size(ref_np)
1048688
You can check that getsizeof and total_size give here the same results (as epxpected, since numpy arrays are not arrays of pointers).
We see that ref_np takes very nearly 1 Byte per element:
total_size(ref_np)/2**20
1.0001068115234375
The size comparison with ref_lst gives:
total_size(ref_lst)/total_size(ref_np)
8.056523961368873
Same as what we get using an array from the array module and an unsigned char encoding.
2.5.5. Q.5
We store ref_lst in numpy packbits array with:
ref_packed = np.packbits(ref_lst)
total_size(ref_packed)
131184
This is expected since each element of ref_packed takes 1 Byte of memory and correspond to 8 successive binary/Boolean elements of ref_lst, the memory size should therefore be very close:
2**20//8
131072
The size comparison with ref_lst gives:
total_size(ref_lst)/total_size(ref_packed)
64.40404317599707
2.5.6. Q.6
We now that 8 successive times are included in a single element of ref_packed, we should therefore get first the result, k, of the target time \(t\) divided (integer division) by 8 (k = t//8), get element k of ref_packed and check if the latter is bit 7-(t-k*8) is one (check stackoverflow Get n-th bit of an integer to see how to do that if you don't know). For the first actual spike time we get:
t1 = idx_lst[0] k1 = t1 // 8 r1 = t1 - k1*8 (ref_packed[k1] >> 7-r1) == 1
True
For the time immediately before:
t2 = idx_lst[0]-1 k2 = t2 // 8 r2 = t2 - k2*8 (ref_packed[k2] >> 7-r2) == 1
False
As an alternative, you can use unpackbits as follows:
(np.unpackbits(ref_packed[k1])[r1] == 1, np.unpackbits(ref_packed[k2])[r2] == 1)
(True, False)
2.6. Solution: Storing spike trains on disk, how and when?
2.6.1. Q.1
We a function run_sim_iid doing the whole simulation plus writing as follows:
def run_sim_iid(rho, ntw_size, n_steps, seed, fname): """Runs an IID simulation of a network with 'ntw_size' neurons a success probability 'rho' for 'n_steps' seeding the PRNG to 'seed' and storing the results in file 'fname' Parameters ---------- rho: a real between 0 and 1 ntw_size: a positive integer n_steps: a positive integer seed: the seed fname: a string Returns ------- Nothing, the function is used for its side effect: a file is opened and the simulation results are stored in it. """ from random import seed if not isinstance(n_steps,int): raise TypeError("n_steps should be an integer.") if not n_steps > 0: raise ValueError("Expecting: n_steps > 0.") sgl_step_iid = mk_sgl_step_iid(rho,ntw_size) with open(fname,"w") as f: for i in range(n_steps): f.write(' '.join(map(str, sgl_step_iid()))+'\n')
We can now time it in the same conditions as before:
print(timeit.timeit('run_sim_iid(0.01, 10**3, 2**20, 20110928, "sim_iid_t1")', number=1, globals=globals()))
66.43105684299371
Two extra seconds is not much to pay.
2.6.2. Q.2
We a function run_sim_iid_np doing the whole simulation plus writing as follows:
def run_sim_iid_np(rho, ntw_size, n_steps, seed, fname): """Runs an IID simulation of a network with 'ntw_size' neurons a success probability 'rho' for 'n_steps' seeding the PRNG to 'seed' and storing the results in file 'fname' Parameters ---------- rho: a real between 0 and 1 ntw_size: a positive integer n_steps: a positive integer seed: the seed fname: a string Returns ------- Nothing, the function is used for its side effect: a file is opened and the simulation results are stored in it. """ if not isinstance(n_steps,int): raise TypeError("n_steps should be an integer.") if not n_steps > 0: raise ValueError("Expecting: n_steps > 0.") sgl_step_iid_np = mk_sgl_step_iid_np(rho,ntw_size,seed) with open(fname,"w") as f: for i in range(n_steps): f.write(' '.join(map(str, sgl_step_iid_np()))+'\n')
We can now time it in the same conditions as before:
print(timeit.timeit('run_sim_iid_np(0.01, 10**3, 2**20, 20110928, "sim_iid_t2")', number=1, globals=globals()))
15.068215111008612
Again, two extra seconds is not much to pay. Keep in mind that we have a very fast "data" generation in this latter case, while in the real setting we will simulate we are going to be closer to the first.
2.7. Solution: Keeping a dynamic window on the past
2.7.1. Using a variable length linked-list
The major "subtlety" is finding out if the indices are present or not, this is done with the in operator:
def sim_with_variable_length_linked_list(n_steps=2**20, rho_success=0.01, tau_max=50): from random import random, randint past = [] t = 0 found_in_past = 0 while t < n_steps: if random() <= rho_success: past.append(t) if len(past) > 0 and past[0] < t-tau_max: past.pop(0) j = randint(0,tau_max) found_in_past += int(t - j in past) k = randint(0,tau_max) found_in_past += int(t - k in past) t += 1 print("Found: " + str(found_in_past)) return found_in_past seed(20061001) print(timeit.timeit('sim_with_variable_length_linked_list()', number=10, globals=globals()))
Found: 20773 Found: 21312 Found: 21316 Found: 20974 Found: 21268 Found: 21059 Found: 20887 Found: 20812 Found: 21493 Found: 20955 20.48626351598068
2.7.2. Using a fixed length linked list based on an array
def sim_with_array_based_fixed_length_linked_list(n_steps=2**20, rho_success=0.01, tau_max=50): from random import random, randint from array import array past = array('B',[0]*(tau_max+1)) t = 0 found_in_past = 0 while t < n_steps: past.pop(0) if random() <= rho_success: past.append(1) else: past.append(0) j = randint(0,tau_max) found_in_past += past[tau_max-j] k = randint(0,tau_max) found_in_past += past[tau_max-k] t += 1 print("Found: " + str(found_in_past)) return found_in_past import timeit from random import seed seed(20061001) print(timeit.timeit('sim_with_array_based_fixed_length_linked_list()', number=10, globals=globals()))
Found: 20773 Found: 21312 Found: 21316 Found: 20974 Found: 21268 Found: 21059 Found: 20887 Found: 20812 Found: 21493 Found: 20955 18.992268898990005
2.7.3. Using a circular buffer
def sim_with_circularlist(n_steps=2**20, rho_success=0.01, tau_max=50): from random import random, randint past = circularlist(tau_max+1) t = 0 found_in_past = 0 while t < n_steps: if random() <= rho_success: past.append(1) else: past.append(0) j = randint(0,tau_max) found_in_past += past[tau_max-j] k = randint(0,tau_max) found_in_past += past[tau_max-k] t += 1 print("Found: " + str(found_in_past)) return found_in_past seed(20061001) print(timeit.timeit('sim_with_circularlist()', number=10, globals=globals()))
Found: 20773 Found: 21312 Found: 21316 Found: 20974 Found: 21268 Found: 21059 Found: 20887 Found: 20812 Found: 21493 Found: 20955 23.96578602300724
2.7.4. Using Binary encoding
def sim_with_binary_past(n_steps=2**20, rho_success=0.01, tau_max=50): from random import random, randint past = 0 n_past = 2**(tau_max+1) t = 0 found_in_past = 0 while t < n_steps: past <<= 1 past %= n_past if random() <= rho_success: past += 1 j = randint(0,tau_max) found_in_past += (past >> j) % 2 k = randint(0,tau_max) found_in_past += (past >> k) % 2 t += 1 print("Found: " + str(found_in_past)) return found_in_past seed(20061001) print(timeit.timeit('sim_with_binary_past()', number=10, globals=globals()))
Found: 20773 Found: 21312 Found: 21316 Found: 20974 Found: 21268 Found: 21059 Found: 20887 Found: 20812 Found: 21493 Found: 20955 19.031911543017486
We see that the best solutions with this parameter set are the fixed length linked list and the binary coding.
For the records, a numpy version, be careful, the function is called only once by the timer!:
def sim_with_binary_past_np(n_steps=2**20, rho_success=0.01, tau_max=50, seed=20061001): import numpy as np rho_success = np.float64(rho_success) rng = np.random.default_rng(seed) past = np.uint64(0) n_past = np.uint64(2**(tau_max+1)-1) one = np.uint64(1) t = 0 found_in_past = 0 while t < n_steps: past = np.left_shift(past,one) past = np.bitwise_and(past,n_past) if rng.random() <= rho_success: past += one j = rng.integers(0,tau_max,dtype=np.uint64,endpoint=True) found_in_past += int(np.bitwise_and(np.right_shift(past, j),one)) k = rng.integers(0,tau_max,dtype=np.uint64,endpoint=True) found_in_past += int(np.bitwise_and(np.right_shift(past, k),one)) t += 1 print("Found: " + str(found_in_past)) return found_in_past import timeit print(timeit.timeit('sim_with_binary_past_np()', number=1, globals=globals()))
Found: 21591 14.47421620201203
3. Representing the model
3.1. Introduction
3.1.1. What is needed to specify a model?
Going back to Sec. 1.5 and 1.6, we see that in the general case a model specification must include:
- n
- the number of neurons in the network (a positive
integer). - edges/synapses properties
- \(\mathbb{W}\)
- an
n x nmatrix of synaptic weights (realelements). - \(\tau_{max}\)
- the largest synaptic delay (a positive or null
integer). - \((\tau_{i \to j})_{i,j \in \{1,\ldots,n\}}\)
- an
n x nmatrix of synaptic delays (positive of nullintegerelements).
- nodes/neurons properties
- \(r_{max}\)
- the largest refractory period (a positive
integer). - \((r_i)_{i \in \{1,\ldots,n\}}\)
- a vector of refractory periods (n positive
integerelements). - \((\phi_i)_{i \in \{1,\ldots,n\}}\)
- a vector of
nspiking probability functions. - \((g_{i \to j})_{i,j \in \{1,\ldots,n\}}\)
- an
n x nmatrix a synaptic leakage functions
3.1.2. What is needed to make the model "advance" in time (generate spike trains)?
In order to advance in time our simulation code must keep track, in the most general case, of (Sec. 1.5.2):
- \(\mathbf{x}_{t}\)
- the realization of the "window on the past", \(\mathbb{X}_{t}\), defined by Eq. \eqref{eq:bigX}, a \(n \times \tau_{max}\) matrix of a vector/list of linked-lists / circular buffers / binary encodings (Sec. 2.4).
- \(\mathbf{v}_{t}\)
- the realization of the present membrane potentials, \(\mathbb{V}_{t}\), defined by Eq. \eqref{eq:bigV}, a vector/list with \(n\) elements.
- \(\mathbf{l}_{t}\)
- the realization of the present "elapsed times since the last spike", \(\mathbb{L}_{t}\), defined by Eq. \eqref{eq:bigL}, a vector/list with \(n\) elements.
3.1.3. Looking for parsimony
Notice that all our "evolution equations"—Eq. \eqref{eq:simple-discrete-V-evolution}, \eqref{def:potential-with-rp}, \eqref{eq:complex-discrete-V-evolution}, \eqref{eq:discrete-V-at-t+1-given}, \eqref{def:potentialwithg}—, consider each neuron \(i\) of the network in turn and, for each \(i\), involve a summation over all the neurons of network. This latter summation can nevertheless be made more efficient if we restrict it to the presynaptic neurons to neuron \(i\): the ones for which \(w_{j \to i} \neq 0\) (or the elements of the set \({\mathcal V}_{ \cdot \to i }\) defined in Sec. 1.1). It is therefore a good idea to include in our model specification:
- \(\left({\mathcal V}_{ \cdot \to i }\right)_{i \in \{1,\ldots,n\}}\)
- a vector/list of lists.
The simulation code will need to have access to these long lists of elements (of very different types). This means that the functions we will have to define will need a lot of input parameters. One way to make our code tidier is then to define a Class whose attributes are the elements we just listed as well as private functions, called methods in the object oriented programming paradigm. An understanding of the class/method mechanism of Python, at the level of Chap. 2 of Goodrich, Tamassia and Goldwasser, Data Structures and Algorithm in Python (2013)—that is, slightly above the level of the Classes section of the official tutorial—, is required in what follows.
3.1.4. More about the rate \(\phi_i\) and leakage \(g_{i \to j}\) functions
We do not necessarily want to have as many different \(\phi_i\) functions as we have neurons in the network or as many different \(g_{i \to j}\) functions as we have actual synapses. In real networks, neurons come in types and in our highly simplified representation it makes sense to identify a type with a rate function, like a \(\phi_{E}\) for excitatory neurons and a \(\phi_{I}\) for inhibitory ones (the latter might be refined if we wanted to add diversity in the inhibitory neurons population). A type would also be associated with a refractory period (\(r_E\) and \(r_i\)) and a self-interaction (if we decide to work with one, \(g_{E}\) and \(g_{I}\)). We would also have as many types of coupling functions \(g_{j \to i}\) for \(j \ne i\) as we have pairs of types: \(E\to E, E \to I, I \to I, I \to I\).
We can therefore reduce the memory used to store a model instance by attaching a label to each neuron specifying its type or kind from a finite set, like \(\mathcal{K} \equiv \{E,I\}\). We then need as many refractory periods and self-interaction functions as we have types and as many coupling functions as the number of types squared. Think about it if we have a network made of 10000 neurons made of 2 types, the potential (memory) saving is huge. We can therefore make our previous "nodes/neurons properties" list more specific by using the types/kinds:
- types
- a tuple representing the \(\mathcal{K}\) set above (e.g.
("E","I")). - \((r_k)_{k \in \mathcal{K}}\)
- the type specific refractory periods.
- \(r_{max}\)
- \(r_{max} \equiv \max_{k \in \mathcal{K}} r_k\).
- \((\phi_k)_{k \in \mathcal{K}}\)
- a vector of \(|\mathcal{K}|\) (the cardinality of set \(\mathcal{K}\)) spiking probability functions.
- \((g_k)_{k \in \mathcal{K}}\)
- a vector of \(|\mathcal{K}|\) self-interaction functions.
- \((g_{i \to j})_{i,j \in \mathcal{K}}\)
- a \(|\mathcal{K}| \times |\mathcal{K}|\) matrix of coupling functions.
3.2. Exercise: Step one, coding the leakage functions \(g_{i \to j}(\,)\)
In the "general case" of Sec. 1.6.2, our code will spend a lot of time evaluating expressions like Eq. \eqref{def:potentialwithg}:
\[V_t (i) = \left\{\begin{array}{lr} \sum_{j \in I} w_{ j \to i} \left( \sum_{ s = L_t (i) + r_i }^{ t} g_{j \to i} (t-s) X_{s- \tau_{j\to i}}(j) \right) , & \text{ if } L_t (i ) < t \\
0, & \text{ if } L_t (i ) = t \end{array}
\right. \]
that require many evaluations of the leakage functions \(g_{i \to j}(\,)\) with a finite support, \(\{0,1,\ldots,t_{max}-1\}\). These functions can be identified with vectors in \(\mathbb{R}^{t_{max}}\), Eq. \eqref{eq:leakage-with-finite-support}:
\[g_{j \to i} (\,) = \left(g_{j \to i}(0), g_{j \to i}(1),\ldots, g_{j \to i}(t_{max}-1)\right) \, .\]
At the implementation level the following question arises: should we use a Python function or an "array" (list, tuple, array of array module, array of numpy) to code these functions? In computer science, such an "array" representation is often referred to as a Lookup table.
You will consider a "pulse" function defined by:
def pulse(t): if 10 <= t < 20: return 1.0 else: return 0.0
You will define list, tuple, array of array module and array of numpy representations of this function on \(\{0,1,\ldots,29\}\) and you will time their evaluations (with timeit) on their full range (that is for every \(i \in \{0,1,\ldots,29\}\)). Conclude.
3.3. Exercise: Step two, dealing with unavoidable function calls \(\phi_i(\,)\)
Even if we do not use models with leakage (Sec. 1.6), our code will need to evaluate many many times the \(\phi_i(\,)\) functions. It is therefore import to reflect a bit on how we can make these calls as "cheap" or fast as possible.
3.3.1. Question 1
Let us for instance consider a simple \(\phi(v)\) function that is linear between \(v_{min}\) and \(v_{max}\) going from 0 to 1, 0 below \(v_{min}\) and 1 above \(v_{max}\). A simple implementation in Python would be:
def phi_linear(v, v_min, v_max): if v < v_min: return 0 if v > v_max: return 1 return (v-v_min)/(v_max-v_min)
Notice that we deliberately avoid parameters checking (v_max should be > v_min for instance) in order to gain speed.
This function could be replaced by:
def phi_linear2(v, v_min, v_max): return min(1,max(0,(v-v_min)/(v_max-v_min)))
These are two different ways to define in Python the same mathematical function.
Compare the times required to evaluate these two functions, as well as a direct evaluation of min(1,max(0,(v-v_min)/(v_max-v_min))) with v_min = 0, v_max = 1 and v taking values in [i/25 fir i in range(26).
In the following questions we will also make the comparison with a slightly more costly \(\phi(\,)\) involving an hyperbolic tangent:
def phi_tanh(v, offset=5, slope=1): from math import tanh return (1.0+tanh((v-offset)*slope))/2
3.3.2. Question 2
It is possible and easy to define C functions that do the same jobs as phi_linear and phi_tanh, to compile them (if you have a C compiler like gcc) and to call them from Python thanks to the functionalities of the ctypes module (this could also be done, resulting in principle in faster codes, with SWIG or Cython, but that's heavy, for me). We could for instance define function phi_c as follows and store this definition in file phi_c.c:
#include <stdlib.h> #include <math.h> double phi_l(double v, double v_min, double v_max) { if (v < v_min) return 0.0; if (v > v_max) return 1.0; return (v-v_min)/(v_max-v_min); } double phi_t(double v, double offset, double slope) { return (1.0+tanh((v-offset)*slope))*0.5; }
We compile the function into a dynamic library with:
gcc -O2 -shared -o phi_c.so -fPIC phi_c.c
In our Python session we import ctypes and 'load' the shared library:
import ctypes as ct _phi_clib = ct.cdll.LoadLibrary('./phi_c.so')
We now have to look at the signature of the functions we want to call, like double phi_c(double v, double v_min, double v_max). Our functions takes 3 floating point numbers in double precision and returns one floating point number is double precision. If the equivalent Python types are not specified, Python assumes essentially that everything is an integer and that's neither the case for the parameters nor for the returned value. We therefore do:
_phi_clib.phi_l.argtypes=[ct.c_double,ct.c_double,ct.c_double] # Parameter types _phi_clib.phi_l.restype = ct.c_double # Returned value type _phi_clib.phi_t.argtypes=[ct.c_double,ct.c_double,ct.c_double] # Parameter types _phi_clib.phi_t.restype = ct.c_double # Returned value type
We can now check that _philib.phi_l gives the same values as phi_linear:
all([_phi_clib.phi_l(i/25,0,1) == phi_linear(i/25,0,1) for i in range(26)])
True
And that _philib.phi_t gives the same values as phi_tanh:
all([_phi_clib.phi_t(i/5,0,1) == phi_tanh(i/5,0,1) for i in range(26)])
True
Make a time comparison between phi_linear and _phi_clib.phi_l, then between phi_tanh and _phi_clib.phi_t like in the former question.
3.3.3. Question 3
We can do the same, more or less, with a Fortran code and numpy F2PY. So we could start by defining subroutines phi_l and phi_t whose definitions are stored in file phi_for.f90:
subroutine phi_l(v, v_min, v_max, rate) real(kind=8), intent(in) :: v, v_min, v_max real(kind=8), intent(out) :: rate if (v < v_min) then rate = 0.0_8 else if (v > v_max) then rate = 1.0_8 else rate = (v-v_min)/(v_max-v_min) end if end subroutine phi_l subroutine phi_t(v, offset, slope, rate) real(kind=8), intent(in) :: v, offset, slope real(kind=8), intent(out) :: rate rate = (1.0_8 + tanh((v-offset)*slope))*0.5_8 end subroutine phi_t
We compile it to make it usable in Python with:
python3 -m numpy.f2py -c phi_for.f90 -m phi_for
We test it against our initial version in the "linear" case:
import phi_for all([phi_for.phi_l(i/25,0,1) == phi_linear(i/25,0,1) for i in range(26)])
True
And in the hyperbolic tangent one:
all([phi_for.phi_t(i/5,0,1) == phi_tanh(i/5,0,1) for i in range(26)])
True
Make a time estimation for phi_for.phi_l and phi_for.phi_t like in the former questions.
3.4. Exercise: Step three, neuron class
Create a Neuron Class, representing individual neurons/edges making the network. This class should have the following attributes:
_idx- the neuron index, a positive or null integer.
_kind- the neuron type, a positive or null integer (we use
kindand nottypebecause the latter is aPythonkeyword). _pre- the set of presynaptic neurons (\({\mathcal V}_{ \cdot \to i }\)) with extra information; a tuple with as many elements as the neuron has presynaptic partners, each element should itself be a tuple with the following elements:
- presynaptic neuron index
- synaptic weight
- synaptic delay
- presynaptic neuron type
The class should define the following methods:
__init__- instance initialization method that should take 3 parameters corresponding to each of the attributes we just defined.
__len__- overloading of the usual
lenfunction that returns the number of presynaptic neurons whenlen(obj)is called andobjis an instance ofNeuron. __getitem__- sub-setting method defined such that
obj[i]returns the i-th presynaptic tuple. idx- returns the Neuron's
_idxattribute (prefix it with a@propertydecorator, so that there is no need to call it withobj.idx(),obj.idxwill do the job). kind- returns the Neuron's
_kindattribute (prefix it with a@propertydecorator). vset- a method that takes a parameter
kind(with defaultNone) and that returns a tuple with the indices of the presynaptic neurons of that kind (all the presynaptic neurons by default).
Since we expect that some of our networks will be made of a lot of neuron, you should define the __slots__ of your class. Make some tests to convince yourself that your implementation is right.
Note The consistency of the _idx, _kind, etc. is going to be ensured by the subsequent classes using Neuron. These classes will be in charge of calling Neuron(idx,kind,pre) in a proper and consistent way. In other words, users of the final code wont have to call Neuron(...), they won't even need to know it exists.
3.5. Exercise: Step four, synaptic graph representation
We continue with a SynapticGraph class that is derived from our previous one Neuron. Fundamentally SynapticGraph is a tuple of Neuron objects with some extra information and dedicated methods. Instances of this class are going to be initialized with an __init__ method taking the following parameters:
- weights
- a list of
nlists ofnelements that specifies the (synaptic) weights \(w_{j \to i}\) as elementweights[j][i]. - delays
- an optional list of
nlists ofnelements that specifies the (synaptic) delays \(\tau_{j \to i}\) as elementdelays[j][i]. It is optional, since by default all the synapttic delays will be considered null. - kinds
- an optional list of
npositive or null integers specifying the kind/type of each neuron. If not specified, all neurons are of the same type. - homogeneity
- a Boolean,
Trueby default, in which case the method checks that all neurons of the same kind/type form synapses of the same sign; e.g. for a model with two kinds of neurons, an excitatory type (0) and an inhibitory one, all the elements ofweight[j]should be positive or null for a neuron of type 0 and negative or null for a neuron of type 1.
Our class should have attributes:
_size- an integer, the number of nodes/neurons of the graph, it should be the common length of
weightsanddelayswhen the latter is specified. This should be checked upon initialization. The fact that none of the sub-list ofweights(anddelaysif specified) is strictly larger thansizeshould also be checked. _nb_types- the number of kinds/types of neurons (we use here
_nb_typesinstead of the more consistent_nb_kinfsbecause our next classNeuronalDynamicswill have the same attribute, that will be called_nb_kinds, and our last class,Network, will inherit from bothSynapticGraphandNeuronalDynamics; we will therefore avoid potential attribute names conflict). _tau_max- an integer, the largest synaptic delay.
_graph- a tuple with
_sizeelements that areNeuronobjects.
It should have the following methods:
nb_types- that returns the value of attribute
_nb_types(prefix it with the@propertydecorator). tau_max- that returns the value of attribute
_tau_max(prefix it with the@propertydecorator). - __getitem__
- that takes an integer,
post, between 0 and_size-1as parameter and that returns the correspondingNeuronobject. - __len__
- that returns the content of
_size. - dot
- that takes an optional list of strings specifying the how the nodes/neurons should be labeled and that returns a string suitable for the content of a Graphviz DOT file satisfying the requirements stated next. By default the labels are going to be "Ni" with i going from 0 to
size-1.
3.5.1. DOT file specification
- The absolute value of the weight should be coded by the arrows thickness (see penwidth in the doc.).
- The value of the delay should be coded by the length of the edge (see weight in the doc.).
- The sign of the weight should be coded by the arrowhead: a positive sign leading to "–>" and a negative one to "–<" (see arrowType in the doc.).
If we have a three neurons, N0, N1, N2, graph such that:
- N0 inhibits N1 with weight -2 and delay 1 and N2 with weight -1 and delay 3.
- N1 excites N0 with weight 1 and delay 3 and N2 with weight 2 and delay 2.
- N2 excites N1 with weight 3 and delay 1.
The content of the string should be someting like:
digraph {
N1 -> N0 [arrowhead=normal penwidth=1 weight=0];
N0 -> N1 [arrowhead=inv penwidth=2 weight=7];
N2 -> N1 [arrowhead=normal penwidth=3 weight=3];
N0 -> N2 [arrowhead=inv penwidth=1 weight=0];
N1 -> N2 [arrowhead=normal penwidth=2 weight=3];
}
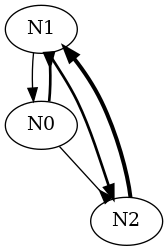 Notice that the representation of the weights magnitude (edge thickness) and delays (edge length) is only qualitative.
Notice that the representation of the weights magnitude (edge thickness) and delays (edge length) is only qualitative.
3.6. Exercise: Step five, neuronal dynamics representation
Instances of class SynapticGraph provide the structure of a network, but a network we can simulate requires a specification of its dynamics, that is:
- \((r_k)_{k \in \mathcal{K}}\)
- the type specific refractory periods.
- \(r_{max}\)
- \(r_{max} \equiv \max_{k \in \mathcal{K}} r_k\).
- \((\phi_k)_{k \in \mathcal{K}}\)
- a vector of \(|\mathcal{K}|\) (the cardinality of set \(\mathcal{K}\)) spiking probability functions.
- \((g_k)_{k \in \mathcal{K}}\)
- a vector of \(|\mathcal{K}|\) self-interaction functions.
- \((g_{i \to j})_{i,j \in \mathcal{K}}\)
- a \(|\mathcal{K}| \times |\mathcal{K}|\) matrix of coupling functions.
We will define a new class, NeuronalDynamics, whose job is to keep and make accessible the above quantities. This class should have the following attributes:
_nb_kinds- a positive integer, the number of kinds/types of neurons.
_r_max- a positive integer, the maximal refractory period; if it is 1, then all neuronal types have the shortest possible refractory period.
_r_tpl- a tuple of null length (if
_r_max = 1) or of length_nb_kinds. _phi_tpl- a tuple of functions of length
_nb_kinds. _t_max- a positive or null integer, the longest coupling/leakage effect; if null, there is no coupling/leakage effect and we are in the setting of Sec. 1.2 to 1.5.
_g_k- a tuple of null length if none of the neuronal kind has a self-interaction term or of length
_nb_kinds; each element should then be a tuple (whose elements do not have to be all of the same sign). _g_2k- a null tuple if
_t_max = 0, or a tuple of_nb_kindstuple; each sub-tuple should then also be a tuple of length_nb_kinds._g_2k[i][j]will contain a tuple with the \(g_{i \to j}\) coupling/leakage effect (Sec. 1.6). If there is coupling between these to neuronal kinds/types then_g_2k[i][j]should be of length_t_max, if there is no coupling, it should be or length 0.
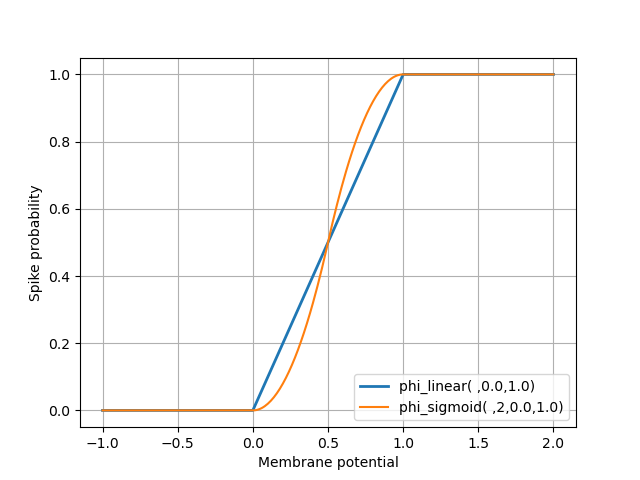
Your class definition should contain the definition of two class functions, not methods, phi_linear and phi_sigmoid:
def phi_linear(v, v_min=0.0, v_max=1.0): x = (v-v_min)/(v_max-v_min) if x < 0.0 : return 0.0 if x <= 1.0: return x else: return 1.0
def phi_sigmoid(v, p=2, v_min=0.0, v_max=1.0): x = 2.0*(v-v_min)/(v_max-v_min) if x < 0.0: return 0.0 if x <= 1.0: return 0.5*x**p if x <= 2.0: return 1.0-0.5*(2-x)**p else: return 1.0
The graphs of these two functions look like:
The following methods should be defined:
rNeuronalDynamics.r(idx)returns the refractory period of kindidx.phiNeuronalDynamics.phi(idx)returns the spiking probability function of neuronal kindidx.g_selfNeuronalDynamics.g_self(idx,t)returns the self-effect of a neuron of kindidx,tsteps after it spiked.g_interactionNeuronalDynamics.g_self(pre,post,t)returns the effect in a neuron of kindpostof a spike from a neuron of kindpre,tsteps after the spike.nb_kinds- that returns the value of attribute
_nb_kinds(prefix it with the@propertydecorator). r_max- that returns the value of attribute
_r_max(prefix it with the@propertydecorator). t_max- that returns the value of attribute
_t_max(prefix it with the@propertydecorator).
3.7. Exercise: Step six, Network class
3.7.1. Outlook
Create a Network class that combines compatible objects of classes SynapticGraph and NetworkDynamics. Here "compatible" means that they should have the same value for their _nb_types / _nb_kinds attributes. The class instances should have everything required to run the simulation. In particular the current state of the system should be managed by the instance and its methods. What makes the state will depend on the network structure—what is contained in the SynapticGraph instance—and on its dynamics—what is contained in the NetworkDynamics instance—. For instance, the state space of simplest network introduced in Sec. 1.4 consist in \(\mathbb{R}^n\) (\(n\), introduced at the beginning of Sec. 1.1, is here the value of attribute _size of the SynapticGraph instance) and its elements were defined by Eq. \eqref{eq:bigV}:
The dynamics is specified by Eq. \eqref{eq:simple-discrete-V-evolution}.
If a non trivial refractory period is introduced (Sec. 1.5.1), the state space must be extended to \((\mathbb{R}^n \times \mathbb{Z}^n)\). We must consider the joint process: \(\left(\mathbb{V}_t,\mathbb{L}_t\right)_{t \geq 0 }\), where the transitions of \(\mathbb{V}_t\) are given by Eq. \eqref{eq:discrete-V-evolution-with-rp} and the transition of \(\mathbb{L}_t\) are given by Eq. \eqref{eq:discrete-L-evolution}. \(\mathbb{L}_t\) is a vector valued random variable defined in Eq. \eqref{eq:bigL}:
\begin{equation*} \mathbb{L}_{t} \equiv \begin{bmatrix} L_t(1) \\ L_t(2) \\ \vdots \\ L_t(n) \end{bmatrix} \end{equation*}If synaptic delays or non geometric, but compact, leakages/couplings are considered (Sec. 1.5.2 and 1.6.2) the state space must be extended further to: \(\mathbb{R}^n \times \mathbb{Z}^n \times \{0,1\}^{n \times (\tau_{max}+t_{max}+1)}\), and we must consider the joint process \((\mathbb{S}_t)_{t \ge 0} \equiv \left(\mathbb{V}_t,\mathbb{L}_t, \mathbb{X}_t\right)_{t \geq 0 }\), where \(\mathbb{X}_t\) is defined by Eq. \eqref{eq:bigX} or \eqref{eq:bigbigX}:
\begin{equation*} \mathbb{X}_{t} \equiv \begin{bmatrix} X_{t-\tau_{max}-t_{max}}(1) & X_{t-\tau_{max}-t_{max}+1}(1) & \cdots & X_{t}(1) \\ X_{t-\tau_{max}-t_{max}}(2) & X_{t-\tau_{max}-t_{max}+1}(2) & \cdots & X_{t}(2) \\ \vdots & \vdots & \ddots & \vdots \\ X_{t-\tau_{max}-t_{max}}(n) & X_{t-\tau_{max}-t_{max}+1}(n) & \cdots & X_{t}(n) \end{bmatrix} \end{equation*}3.7.2. Class attributes
Your Network objects should therefore have the following extra "private" attribute (they will also have the attributes of the two classes they are derived from):
_t_now- the time (step) reached by the simulation.
_past_len- the length of the past to consider,
SynapticGraph._tau_max + NetworkDynamics._t_max _V- an array (of module array) of doubles with
_sizeelements, it will contain \(\mathbb{V}_{t}\). _L- an array of signed long integers with either no elements (if
_r_maxis 1) or with_sizeelements, it will contain \(\mathbb{L}_{t}\). _X- a tuple of unsigned char arrays; the tuple will be of null length if there is no synaptic delay and no leakage or of length
_size. Its elements when the tuple has an actual content will be arrays of size_t_max + _tau_max + 1. This attribute will contain \(\mathbb{X}_{t}\).
3.8. Solution: Step one, coding the leakage functions \(g_{i \to j}(\,)\)
This is simply done with:
g_v = [pulse(i) for i in range(30)] g_t = tuple(g_v) from array import array g_a = array('d',g_v) import numpy as np g_np = np.array(g_v) import timeit print('Function call:') print(timeit.timeit('[pulse(i) for i in range(30)]',globals=globals())) print('List call:') print(timeit.timeit('[g_v[i] for i in range(30)]',globals=globals())) print('Tuple call:') print(timeit.timeit('[g_t[i] for i in range(30)]',globals=globals())) print('Array call:') print(timeit.timeit('[g_a[i] for i in range(30)]',globals=globals())) print('Numpy array call:') print(timeit.timeit('[g_np[i] for i in range(30)]',globals=globals()))
Function call: 3.921000216039829 List call: 1.5582613400183618 Tuple call: 1.5574196510133334 Array call: 1.769933488976676 Numpy array call: 3.4350543709588237
The most efficient representations are the list and tuple.
3.9. Solution: Step two, dealing with unavoidable function calls \(\phi_i(\,)\)
3.9.1. Q.1
This is simply done with:
import timeit left = 0 right = 1 print('phi_linear call:') print(timeit.timeit('[phi_linear(i/25,left,right) for i in range(25)]',globals=globals())) print('phi_linear2 call:') print(timeit.timeit('[phi_linear2(i/25,left,right) for i in range(25)]',globals=globals())) print('Direct estimation:') print(timeit.timeit('[min(1,max(0,(i/25-left)/(right-left))) for i in range(25)]',globals=globals()))
phi_linear call: 6.551414999004919 phi_linear2 call: 10.65268645301694 Direct estimation: 8.990929204970598
3.9.2. Q.2
The locally linear functions are simply compared with:
import timeit left = 0 right = 1 print('phi_linear call:') print(timeit.timeit('[phi_linear(i/25,left,right) for i in range(25)]',globals=globals())) print('_phi_clib.phi_l call:') print(timeit.timeit('[_phi_clib.phi_l(i/25,left,right) for i in range(25)]',globals=globals()))
phi_linear call: 6.389747657987755 _phi_clib.phi_l call: 22.24291676498251
The hyperbolic tangent based functions give:
import timeit left = 0 right = 1 print('phi_tanh call:') print(timeit.timeit('[phi_tanh(i/5,left,right) for i in range(25)]',globals=globals())) print('_phi_clib.phi_t call:') print(timeit.timeit('[_phi_clib.phi_t(i/5,left,right) for i in range(25)]',globals=globals()))
phi_tanh call: 30.951816001033876 _phi_clib.phi_t call: 24.338442599982955
3.9.3. Q.3
This is simply done with:
import timeit left = 0 right = 1 print('phi_for.phi_l call:') print(timeit.timeit('[phi_for.phi_l(i/25,left,right) for i in range(25)]',globals=globals())) print('phi_for.phi_t call:') print(timeit.timeit('[phi_for.phi_t(i/5,left,right) for i in range(25)]',globals=globals()))
phi_for.phi_l call: 7.309892535035033 phi_for.phi_t call: 8.534695383976214
3.10. Solution: Step three, neuron class
3.10.1. <<Neuron Class>>
The class skeleton is:
class Neuron: <<Neuron-doc>> __slots__ = '_idx', '_kind', '_pre' <<Neuron-init>> <<Neuron-len>> <<Neuron-getitem>> <<Neuron-vset>> @property def idx(self): return self._idx @property def kind(self): return self._kind
3.10.2. <<Neuron-doc>>
The class docstring:
"""A neuron representing class. A Neuron object has the following 'private' attributes: - _idx: its index (positive or null integer) that uniquely identifies it. - _kind: its kind/type (positive or null integer) - _pre: a tuple with as many elements as the neuron receives presynaptic inputs. Each element is itself a tuple with 4 elements: - pre_idx: the index of the presynaptic neuron - pre_weight: the weight of the synapse (a real number) - pre_delay: the synaptic delay (positive or null integer) - pre_kind: the presynaptic neuron kind/type. The class has the following methods: - __init__: the constructor (not supposed to be called directly by the user). - idx: returns the Neuron's _idx attribute (can be called with obj.idx). - kind: returns the Neuron's _kind attribute (can be called with obj.kind). - len: returns the number of presynaptic neurons. - []: Neuron[idx] returns the tuple of presynaptic neuron 'idx' - vset: returns the list of indices of presynaptic neurons (potentially depending on their kind/type). """
3.10.3. <<Neuron-init>>
We define here the special method __init__ that gets called upon class instance creation. We give it as parameters idx (default 0), kind (default 0) and pre (default (), an empty tuple):
def __init__(self,idx=0, kind=0, pre=()): """Initializes a Neuron. Parameters ---------- idx: positive or null integer, the neuron index within the network. kind: positive or null integer, the neuron kind/type. pre: an iterable of tuples (pre_idx, pre_weight, pre_delay, pre_kind) where 'pre_idx' is the index of the presynaptic neuron, 'pre_weight' is the weight of the synapse, 'pre_delay', is the synaptic delay, 'pre_kind', is the presynaptic kind/type. All the 'pre_idx' should be different. Returns ------- Nothing but attributes: _idx, _kind and _pre are initialized. """ from collections.abc import Iterable if not isinstance(idx,int): raise TypeError('idx must be an integer.') if idx < 0: raise ValueError('idx must be >= 0.') self._idx = idx if not isinstance(kind,int): raise TypeError('kind must be an integer.') if kind < 0: raise ValueError('kind must be >= 0.') self._kind = kind if not isinstance(pre,Iterable): raise TypeError('pre must be an Iterable.') if len(pre) > 0: if not all([isinstance(p,tuple) for p in pre]): raise ValueError('pre must contain tuples.') if not all([len(p)==4 for p in pre]): raise ValueError('pre must contain tuples of length 4.') if not all([all([isinstance(p[0],int),isinstance(p[1],float) or isinstance(p[1],int), isinstance(p[2],int),isinstance(p[3],int)]) for p in pre]): raise ValueError('pre must contain (int,float,int,int) tuples.') if any([any([p[0] < 0, p[2] < 0, p[3] < 0]) for p in pre]): raise ValueError('pre must contain tuples with positive or null first, third and fourth elements.') if len(set([p[0] for p in pre])) != len(pre): raise ValueError('All first elements of the pre tuples should be different.') self._pre = tuple([t for t in pre])
3.10.4. <<Neuron-len>>
This block defines the special method __len__ that makes the syntax len(obj) meaningful for an object of class Neuron by returning its number of presynaptic partners:
def __len__(self): """Returns the number of presynaptic partners.""" return len(self._pre)
3.10.5. <<Neuron-getitem>>
This block defines the special method __getitem__ that makes the syntax obj[i] meaningful for an object of class Neuron:
def __getitem__(self,idx): """Returns the tuple of presynaptic neuron 'idx'.""" return self._pre[idx]
3.10.6. <<Neuron-vset>>
def vset(self,kind=None): """Returns a tuple with the indices of presynaptic neurons with kind 'kind'. Parameters ---------- kind: a positive or null integer. Returns ------- A tuple with indices of presynaptic neurons """ if not kind is None: if not isinstance(kind,int): raise TypeError('kind must be an integer.') if kind < 0: raise ValueError('kind must be >= 0.') res = [p[0] for p in self if p[3] == kind] else: res = [p[0] for p in self] return tuple(res)
3.10.7. Some tests
Naive instantiation:
n1 = Neuron() len(n1)
0
More interesting a neuron with 3 presynaptic partners:
n2 = Neuron(1,0,[(0,0.5,1,0),(2,-0.5,2,1),(3,0.25,0,0)]) len(n2)
3
Let us look at the synaptic weights:
[t[1] for t in n2]
[0.5, -0.5, 0.25]
We can check vset with any of those:
n2.vset() # (0, 2, 3) n2.vset(0) # (0, 3) n2.vset(1) # (2,) n2.vset(2) # ()
Let us check that our checks work with any of:
n3 = Neuron(-1) # ValueError n3 = Neuron(2,-1) # ValueError n3 = Neuron(2,1,(0)) # TypeError n3 = Neuron(2,1,(0,0)) # ValueError n3 = Neuron(2,1,((0,),(0,))) # ValueError n3 = Neuron(2,1,((0,1,2,3),(-1,1,2,3))) # ValueError n3 = Neuron(1,0,[(0,0.5,1,0),(2,-0.5,2,1),(2,0.25,0,0)]) # ValueError
3.11. Solution: Step four, synaptic graph representation
3.11.1. SynapticGraph Class
The class skeleton is:
class SynapticGraph: <<SynapticGraph-doc>> <<SynapticGraph-init>> <<SynapticGraph-getitem>> <<SynapticGraph-len>> <<SynapticGraph-dot>> @property def nb_types(self): return self._nb_types @property def tau_max(self): return self._tau_max
3.11.2. <<SynapticGraph-doc>>
The class docstring:
"""A Synaptic graph class. Objects of this class are essentially tuples of Neuron objects. SynapticGraph objects have th dollowing 'private' attributes: - _size: a postive integer, the nuber of neurons in the graph/network. - _nb_types: a postive integer, the nuber of neuron kinds/types. - _tau_max: a positive or null integer, the largest synaptic delay. - _graph: a tuple of '_size' Neuron objects. The following methods are defined: - __init__: the class constructor (meant to be called by the user). - nb_types: returns the value of attribute _nb_types (called with obj.nb_types). - tau_max: returns the value of attribute _tau_max (called with obj.tau_max). - len: returns the number of neurons in the graph. - []: SynapticGraph[idx] returns the corresponding Neuron object. - dot: returns a string suitable for generating a graphical representation of the graph with GraphViz. """
3.11.3. <<SynapticGraph-init>>
We define here the special method __init__ that gets called upon class instance creation. We give it as parameters weights and delays (optional).
def __init__(self, weights, delays=[], kinds=[], homogeneity=True): """Initializes instances of class SynapticGraph. Parameters ---------- weights: a list of sub-lists. There are as many sub-lists as nodes/neurons in the directed graph. Each sub-list is as long as the parent list. The elements are real. The first index correspond to the pre- synaptic neuron, the second, to the postsynaptic. delays: an optional list of sub-lists. There are as many sub- lists as nodes/neurons in the directed graph. Each sub- list is as long as the parent list. The elements are positive or null integers. The first index correspond to the presynaptic neuron, the second, to the postsynaptic. If not specified all delays are 0. kinds: an optional list of postive or null integer specifying the kind/type of each neuron. There as many elements as neurons. If not specified, all the neurons are of the same kind. homogeneity: a Boolean, if True (default) the code checks that all neurons of the same kind form synapses with the same sign. Returns ------- Nothing but attributes: size and graph get initialized. """ from collections.abc import Iterable import numbers # Check weights <<SynapticGraph-check-weights>> # Check delays <<SynapticGraph-check-delays>> <<SynapticGraph-check-kinds>> <<SynapticGraph-check-homogeneity>> <<SynapticGraph-graph-attribute>>
3.11.3.1. <<SynapticGraph-check-weights>>
This block checks that the list of lists, weights, corresponds to a properly defined connection matrix. It also initializes attribute _size (containing the network size):
if not isinstance(weights,Iterable): # Check that 'weights' is iterable raise TypeError('weights must be an iterable.') self._size = len(weights) if not all([len(lst)==self._size for lst in weights]): raise ValueError("weights should contain " + str(self._size) + \ " lists of length " + str(self._size)) if not all([all([isinstance(w,numbers.Number) for w in weights[i]]) \ for i in range(self._size)]): raise ValueError("weights elements should all numbers")
3.11.3.2. <<SynapticGraph-check-delays>>
This block checks that the list of lists, delays, corresponds to a properly defined delay matrix:
if delays != []: if not isinstance(delays,Iterable): # Check that 'delays' is iterable raise TypeError('delays must be an iterable.') if not len(delays) == self._size: raise ValueError('delays and weights should have the same length') if not all([len(lst)==self._size for lst in delays]): raise ValueError("delays should contain " + str(self._size) +\ " lists of length " + str(self._size)) if not all([all([type(d) == int for d in delays[i]]) for i in range(self._size)]): raise TypeError("delays elements should all integers") if not all([all([d >= 0 for d in delays[i]]) for i in range(self._size)]): raise ValueError("delays elements should all non negative") self._tau_max = max(max(delays)) else: self._tau_max = 0
3.11.3.3. <<SynapticGraph-check-kinds>>
This block checks that the list, kinds, corresponds to a proper kind/type specification:
if kinds != []: if not isinstance(kinds,Iterable): # Check that 'kinds' is iterable raise TypeError('kinds must be an iterable.') if not len(kinds) == self._size: raise ValueError('kinds and weights should have the same length') if not all([isinstance(k,int) for k in kinds]): raise TypeError("kinds elements should all integers") if not all([k >= 0 for k in kinds]): raise ValueError("kinds elements should all non negative") self._nb_types = len(set(kinds)) else: self._nb_types = 1
3.11.3.4. <<SynapticGraph-check-homogeneity>>
This block checks that each neuron forms synapse with the same sign and that all neurons of the same kind/type form synapses of the same sign:
if homogeneity: kind_sign = [0]*self._nb_types for n_idx in range(self._size): n_pos = 0 n_neg = 0 for p_idx in range(self._size): if weights[n_idx][p_idx] > 0: n_pos += 1 if weights[n_idx][p_idx] < 0: n_neg += 1 if n_pos > 0 and n_neg > 0: raise ValueError('Neuron ' + str(n_idx) + ' is both excitatory and inhibitory.') if kind_sign[kinds[n_idx]] != 0: if n_pos > 0 and kind_sign[kinds[n_idx]] == -1: raise ValueError('Nonhomogeneous neuron types.') if n_neg > 0 and kind_sign[kinds[n_idx]] == 1: raise ValueError('Nonhomogeneous neuron types.') else: if n_pos > 0: kind_sign[kinds[n_idx]] = 1 if n_neg > 0: kind_sign[kinds[n_idx]] = -1
3.11.3.5. <<SynapticGraph-graph-attribute>>
This block sets attribute graph of the instance after constructing it:
graph = [] if kinds == []: kinds = [0]*self._size for post_idx in range(self._size): pre = [] for pre_idx in range(self._size): w = weights[pre_idx][post_idx] if w != 0: lst = [pre_idx,w] if self._tau_max != 0: lst.append(delays[pre_idx][post_idx]) else: lst.append(0) lst.append(kinds[pre_idx]) pre.append(tuple(lst)) #breakpoint() graph.append(Neuron(post_idx,kinds[post_idx],pre)) self._graph = tuple(graph)
3.11.4. <<SynapticGraph-getitem>>
This block defines the special method __getitem__ that makes the syntax myobj[i] meaningful for an object of class SynapticGraph:
def __getitem__(self,idx): """Returns the tuple of presynaptic neuron triplets to neuron 'idx'.""" return self._graph[idx]
3.11.5. <<SynapticGraph-len>>
This block defines the special method __len__ that makes the syntaxe len(myobj) meaningful for an object of class SynapticGraph by returning the network size:
def __len__(self): """Returns the network size.""" return self._size
3.11.6. <<SynapticGraph-dot>>
This block defines the dot method:
def dot(self,labels=[]): """Returns a string corresponding to the content of a DOT file suitable for generating a graphical representation. Parameters ----------- labels: a list of strings, each element will be the label of one node/neuron of the graph. There should be as many elements as there are nodes/neurons. If left unspecified the labels are N0, N1, ... Returns -------- A string. """ if labels == []: labels = ["N"+str(i) for i in range(len(self))] txt = "digraph {\n" for post in range(len(self)): neuron = self[post] for pre_idx in range(len(neuron)): idx = neuron[pre_idx][0] line = "N"+str(idx)+" -> N"+str(post)+" [" if neuron[pre_idx][1] > 0: line += "arrowhead=normal " else: line += "arrowhead=inv " line += "penwidth="+str(abs(round(neuron[pre_idx][1])))+" " if self._tau_max > 0: w = 10*(1-neuron[pre_idx][2]/self.tau_max) line += "weight="+str(round(w)) line += "];\n" txt += line txt += "}\n" return txt
3.11.7. Tests
Using the simple 3 neurons graph of the above example we do:
sg3 = SynapticGraph([[0,-2,-1],[1,0,2],[0,3,0]], [[0,1,3],[3,0,2],[0,1,0]], [1,0,0]) [tpl for tpl in sg3[1]]
[(0, -2, 1, 1), (2, 3, 1, 0)]
We can reproduce the previous graphical representation with:
with open("test-dot-for-SynapticGraph.dot","w") as f: f.write(sg3.dot())
Followed by the following instructions from the command line assuming that dot has been installed:
dot -Tpng test-dot-for-SynapticGraph.dot > test-dot-for-SynapticGraph.png
3.12. Solution: Step five, neuronal dynamics representation
3.12.1. NeuronalDynamics Class
The class skeleton is:
class NeuronalDynamics: <<NeuronalDynamics-doc>> <<phi_linear>> <<phi_sigmoid>> <<NeuronalDynamics-init>> <<NeuronalDynamics-r>> <<NeuronalDynamics-phi>> <<NeuronalDynamics-g_self>> <<NeuronalDynamics-g_interaction>> @property def nb_kinds(self): return self._nb_kinds @property def r_max(self): return self._r_max @property def t_max(self): return self._t_max
3.12.2. <<NeuronalDynamics-doc>>
The class docstring:
"""Required properties for specifying network dynamics. The class 'private' attributes are: - _nb_kinds: the number of neuron kinds/types (positive integer). - _phi_tpl: a tuple of lenghth '_nb_kinds'. The spiking probability function of each neuronal kind/type. - _rho_tpl: a tuple of lenghth 0 or '_nb_kinds'. In the latter case, each tuple element, rho, is such that 0 < rho < 1 and specifies a 'geometrical' leakage; that is, in the abscence of input the membrane potentials at two successive steps satisfy: v[t+1] = rho*v[t] - _r_max: the longest refractory period (positive integer). - _r_tpl: a tuple of length 0 (if '_r_max'=1) or '_nb_kinds'. In the latter case, the refractory periods of each neuronal kind/type. - _g_k: a tuple of tuples describing the self_interactions of the neurons of each neuronal kind/type. Can be of null length in the absence of self-interaction. - _g_2k: a tuple of tuples of tuples describing the interactions between two neurons of two given kinds/types. Can be of null length if there is no leakage. The class contains two functions that can be used to build spiking probability functions: - phi_linear - phi_sigmoid The class defines the following methods: - r: NeuronalDynamics.r(idx) returns the refractory period of kind 'idx'. - phi: NeuronalDynamics.phi(idx) returns the spiking probability function of kind 'idx'. - g_self: NeuronalDynamics.g_self(idx,t) returns the self-effect of a neuron of kind 'idx', 't' steps after it spiked. - g_interaction: NeuronalDynamics.g_self(pre,post,t) returns the effect of a spike from a neuron of kind 'pre' 't' steps after the spike in a neuron of kind 'post'. - nb_kinds: returns the value of attribute _nb_kinds (called with obj.nb_kinds). - r_max: returns the value of attribute _r_max (called with obj.r_max). - t_max: returns the value of attribute _t_max (called with obj.t_max). """
3.12.3. <<NeuronalDynamics-init>>
def __init__(self, nb_kinds=1, phi_tpl=(), rho_tpl=(), r_tpl=(), g_k=(), g_2k=()): from warnings import warn <<NeuronalDynamics-init-nb_kinds>> <<NeuronalDynamics-init-phi_tpl>> if not isinstance(rho_tpl,tuple): raise TypeError('rho_tpl should be a tuple.') if len(rho_tpl) != 0: if not len(rho_tpl) == self._nb_kinds: raise TypeError('rho_tpl should have length ' + str(nb_kinds) + ".") if not all([0 < rho < 1 for rho in rho_tpl]): raise ValueError('rho_tpl elements should be > 0 and < 1.') self._rho_tpl = rho_tpl self._r_max = 1 self._r_tpl = () self._g_k = () self._g_2k = () else: self._rho_tpl = () <<NeuronalDynamics-init-r_tpl>> <<NeuronalDynamics-init-g_k>> <<NeuronalDynamics-init-g_2k>>
3.12.3.1. <<NeuronalDynamics-init-nb_kinds>>
Checks validity of parameter nb_kind and sets attribute _nb_kinds:
if not isinstance(nb_kinds,int): raise TypeError('nb_kinds should be an integer.') if nb_kinds < 1: raise ValueError('nb_kinds should be >= 1.') self._nb_kinds=nb_kinds
3.12.3.2. <<NeuronalDynamics-init-phi_tpl>>
This code block checks the validity of parameter phi_tpl. If an empty list, it sets attribute _phi_tpl to a tuple of nb_kinds copies of NeuronalDynamics.phi_linear. If not an empty list, it checks that each element is a function and that it return a value between 0 and 1 for an input range of [-5,5]:
if not isinstance(phi_tpl,tuple): raise TypeError('phi_tpl should be a tuple.') if len(phi_tpl) == 0: self._phi_tpl = tuple([NeuronalDynamics.phi_linear for i in range(nb_kinds)]) else: if not len(phi_tpl) == self._nb_kinds: raise TypeError('phi_tpl should have length ' + str(nb_kinds) + ".") vv = [i/10 for i in range(-50,51)] for idx in range(self._nb_kinds): if not callable(phi_tpl[idx]): raise TypeError('phi_tpl['+str(idx)+'] should be callable.') if not all([0 <= phi_tpl[idx](v) <= 1 for v in vv]): raise ValueError('phi_tpl['+str(idx)+'] should take values in [0,1].') self._phi_tpl = phi_tpl
3.12.3.3. <<NeuronalDynamics-init-r_tpl>>
This block checks the validity of parameter r_tpl and sets attribute _r_tpl:
if not isinstance(r_tpl,tuple): raise TypeError('r_tpl should be a tuple.') if len(r_tpl) == 0: self._r_max = 1 self._r_tpl = () else: r_max = 0 if not len(r_tpl) == self._nb_kinds: raise TypeError('r_tpl should have length ' + str(nb_kinds) + ".") for idx in range(self._nb_kinds): if not isinstance(r_tpl[idx],int): raise TypeError('r_tpl['+str(idx)+'] should be an integer.') if r_tpl[idx] < 1: raise ValueError('r_tpl['+str(idx)+'] should be >= 1.') if r_tpl[idx] > r_max: r_max = r_tpl[idx] self._r_max = r_max self._r_tpl = r_tpl
3.12.3.4. <<NeuronalDynamics-init-g_k>>
This block checks the validity of parameter g_k and sets attribute _g_k. The elements of g_k do not have to be all of the same length, an element can even be an empty tuple, (), but the attribute _g_k will contain _nb_kind tuples all of the same length corresponding to the largest length among the elements of g_k. When an element of g_k is smaller than the longest, it is made longer with null elements. This block also defines tau_set, a local variable, used in the next code block.
tau_max = 0 tau_set = False if not isinstance(g_k,tuple): raise TypeError('g_k should be a tuple.') if len(g_k) == 0: self._g_k = () else: if not len(g_k) == self._nb_kinds: raise TypeError('g_k should have length ' + str(nb_kinds) + ".") tau_max = max([len(g) for g in g_k])-1 tau_set = True if not all([isinstance(g,tuple) for g in g_k]): raise TypeError('Every element of g_k should be a tuple.') g_k_u = [] for g in g_k: if len(g) == tau_max + 1: g_k_u.append(g) else: g_k_u.append(tuple(list(g) + [0]*(tau_max + 1-len(g)))) self._g_k = tuple(g_k_u)
3.12.3.5. <<NeuronalDynamics-init-g_2k>>
This block checks the validity of parameter g_2k and sets attribute _g_2k. It also issues a warning if the sum of the g_2k[i][j] is different from 1. The idea behind this point is that the synaptic weight should be used to set the synaptic strength and g_2k[i][j] just describes the time course. Like in the previous block, elements of g_2k do not have to be all of the same length, they are made longer with null elements if necessary.
if not isinstance(g_2k,tuple): raise TypeError('g_2k should be a tuple.') if len(g_2k) == 0: self._g_2k = () else: if not len(g_2k) == self._nb_kinds: raise TypeError('g_2k should have length ' + str(nb_kinds) + ".") g_2k_nb_max = 0 for pre_idx in range(self._nb_kinds): if not isinstance(g_2k[pre_idx],tuple): raise TypeError('g_2k['+str(pre_idx)+'] should be a tuple.') if not len(g_2k[pre_idx]) == self._nb_kinds: raise TypeError('g_2k['+str(pre_idx)+'] should have length ' + str(nb_kinds) + '.') for post_idx in range(self._nb_kinds): if not isinstance(g_2k[pre_idx][post_idx],tuple): raise TypeError('g_2k['+str(pre_idx)+']['+\ str(post_idx)+'] should be a tuple.') nb = len(g_2k[pre_idx][post_idx]) if nb > g_2k_nb_max: g_2k_nb_max = nb if tau_set: if g_2k_nb_max > tau_max + 1: # make elements of _g_k longer g_k_u = [] for g in self._g_k: g_k_u.append(tuple(list(g)+[0]*(g_2k_nb_max-tau_max-1))) self._g_k = tuple(g_k_u) tau_max = g_2k_nb_max - 1 else: tau_max = g_2k_nb_max - 1 g_2k_u = [] for pre_idx in range(self._nb_kinds): g_pre_post = [] for post_idx in range(self._nb_kinds): g = g_2k[pre_idx][post_idx] nb = len(g) if nb <= tau_max: g_pre_post.append(tuple(list(g)+[0]*(tau_max+1-nb))) else: g_pre_post.append(g) if abs(sum(g)-1.0) > 1e-6 and abs(sum(g)) > 1e-6: warn('The sum of g_2k['+str(pre_idx)+']['+\ str(post_idx)+'] is not 0.0 or 1.0.') g_2k_u.append(tuple(g_pre_post)) self._g_2k = tuple(g_2k_u) self._t_max = tau_max
3.12.4. <<NeuronalDynamics-r>>
This methods returns the refractory period of kind/type idx:
def r(self,idx): """Refractory period of kind/type 'idx'.""" if self.r_max == 1: return 1 if not (0 <= idx < self.nb_kinds): raise ValueError('Must have 0 <= idx < ' + str(self.nb_kinds) + '.') else: return self._r_tpl[idx]
3.12.5. <<NeuronalDynamics-phi>>
This method returns the spiking probability function of kind/type idx:
def phi(self,idx): """Spiking probability function of kind/type 'idx'.""" if not (0 <= idx < self.nb_kinds): raise ValueError('Must have 0 <= idx < ' + str(self.nb_kinds) + '.') else: return self._phi_tpl[idx]
3.12.6. <<NeuronalDynamics-g_self>>
This method returns the "self-interaction" of kind idx at delay of t time steps after a spike:
def g_self(self,idx,t): """Self interaction of kind/type 'idx' at 't'.""" if self.t_max == 0: return 0.0 if not (0 <= idx < self.nb_kinds): raise ValueError('Must have 0 <= idx < ' + str(self.nb_kinds) + '.') else: if not 0 <= t <= self.t_max: return 0.0 else: return self._g_k[idx][t]
3.12.7. <<NeuronalDynamics-interaction>>
This method returns the effect of a spike from a neuron of kind/type pre_idx in a neuron of kind/type post_idx after a delay of t time steps:
def g_interaction(self, pre_idx, post_idx, t): """Interaction of kind 'pre_idx' with 'post_idx' at 't'.""" if self.t_max == 0: return 1.0 if post_idx == pre_idx: return self.g_self(pre_idx,t) if not (0 <= pre_idx < self.nb_kinds): raise ValueError('Must have 0 <= pre_idx < ' + str(self.nb_kinds) + '.') if not (0 <= post_idx < self.nb_kinds): raise ValueError('Must have 0 <= post_idx < ' + str(self.nb_kinds) + '.') if not 0 <= t <= self.t_max: return 0.0 else: return self._g_2k[pre_idx][post_idx][t]
3.12.8. Tests
3.12.8.1. Using defaults
dyn1 = NeuronalDynamics() print("The refractory period of kind/type 0 is: " + str(dyn1.r(0)) + ".") print("The value of tau_max is: " + str(dyn1._t_max) + ".") print("The spiking probability at 0.5 is: " + str(dyn1.phi(0)(0.5)) + ".")
The refractory period of kind/type 0 is: 1. The value of tau_max is: 0. The spiking probability at 0.5 is: 0.5.
3.12.8.2. Setting phi_tpl
dyn2 = NeuronalDynamics(phi_tpl = (lambda v: NeuronalDynamics.phi_sigmoid(v,v_min=-0.1),)) print("The refractory period of kind/type 0 is: " + str(dyn2.r(0)) + ".") print("The spiking probability at 0.0 is: " + str(dyn2.phi(0)(0.0)) + ".")
The refractory period of kind/type 0 is: 1. The spiking probability at 0.0 is: 0.01652892561983471.
3.12.8.3. Setting an inappropriate phi_tpl
dyn0 = NeuronalDynamics(phi_tpl = (0.5,)) # TypeError phi_tpl[0] not callable dyn0 = NeuronalDynamics(phi_tpl = (lambda v: v,)) # ValueError phi_tpl[0] values out of [0,1]
3.13. Solution: Step six, Network class
3.13.1. Network Class
The class skeleton is:
class Network(SynapticGraph,NeuronalDynamics): <<Network-doc>> array = __import__('array') <<Network-init>> @property def t_now(self): return self._t_now @property def past_len(self): return self._past_len <<Network-spike-prob>> <<Network-update_nl_simple>>
3.13.2. <<Network-doc>>
"""A neural network class. Class instances inherit from SynapticGraph and from NeuronalDynamics classes. They contains all the information about the structure (SynapticGraph) and about the dynamics (NeuronalDynamics). They keep in addition the Network state information in dedicated attributes: _V: the membrane voltage of each neuron, an array.array of real numbers. _L: if necessary, the time (step) of the last spike from each neuron, an array.array of integers. _X: if necessary, a tuple of array.array of unsigend chars containing the spike train of eah neuron few time steps in the past. _past_len: the length of the past to keep, a postive or null integer. _t_now: the current time step. """
3.13.3. <<Network-init>>
Class docstring;
def __init__(self, SG_obj, ND_obj, V0 = None, L0 = None, X0 = None): <<Network-init-doc>> from collections.abc import Iterable <<Network-check-SG_obj-ND_obj>> <<Network-set-inherited-attributes>> self._past_len = ND_obj.t_max + SG_obj.tau_max <<Network-set-_V-attribute>> <<Network-set-_L-attribute>> <<Network-set-_X-attribute>> self._t_now = 0
3.13.3.1. <<Network-init-doc>>
__init__ method docstring:
"""Network class constructor. Parameters ---------- SG_obj: a SynapticGraph object whose _nb_types value must be identical to the _nb_kinds value of 'ND_obj'. ND_obj: a NeuronalDynamics object whose _nb_kinds value must be identical to the _nb_types value of 'SG_obj'. V0: initial membrane potential values of the neurons, an optional iterable with the 'right' length. If not specified all neurons start at 0. L0: initial value of the last spike time, an optional iterable with the 'right' length. If not specified all neurons start at 0, meaning that they just all spiked. X0: intial value of the spike history of each neuron, an optional iterable with the 'right' lenght. Each element should itself be an iterable with the right length. If not specified the minimal history consistent with 'L0' is provided. If both 'L0' and 'X0' are specified, their consistency is checked. Returns ------- Nothing the constructor is called for its side effect, a Network instance is created. """
3.13.3.2. <<Network-check-SG_obj-ND_obj>>
This block checks that SG_obj is a SynapticGraph object, that ND_obj is a NeuronalDynamics objects and that attribute _nb_types of the former has the same value as attribute _nb_kinds of the latter:
if not isinstance(SG_obj,SynapticGraph): raise TypeError("SG_obj should be an instance of SynapticGraph.") if not isinstance(ND_obj,NeuronalDynamics): raise TypeError("ND_obj should be an instance of NeuronalDynamics.") if SG_obj.nb_types != ND_obj.nb_kinds: raise ValueError("SG_obj _nb_types should be the same as and ND_obj _nb_kinds attribute.")
3.13.3.3. <<Network-set-inherited-attributes>>
This block sets attributes inherited from SG_obj (a SynapticGraph object) and ND_obj (a NeuronalDynamics object):
self._size = len(SG_obj) self._nb_types = SG_obj.nb_types self._nb_kinds = ND_obj.nb_kinds self._tau_max = SG_obj.tau_max self._graph = SG_obj._graph self._rho_tpl = ND_obj._rho_tpl self._r_max = ND_obj.r_max self._r_tpl = ND_obj._r_tpl self._phi_tpl = ND_obj._phi_tpl self._t_max = ND_obj.t_max self._g_k = ND_obj._g_k self._g_2k = ND_obj._g_2k
3.13.3.4. <<Network-set-_V-attribute>>
Sets attribute _V with a default of 0 for each neuron if parameter V0 is not given:
if V0 is None: self._V = self.array.array('d',[0]*len(SG_obj)) else: if not isinstance(V0,Iterable): raise TypeError('V0 must be an Iterable.') if not len(V0) == len(SG_obj): raise TypeError('V0 length should be ' + str(len(SG_obj)) +'.') self._V = self.array.array('d',V0)
3.13.3.5. <<Network-set-_L-attribute>>
This block sets _L attribute. If L0 is not specified and if a non zero length _L is required by the model, all elements are set to 0, meaning that all the neurons of the network just spiked.
if ND_obj.r_max > 1: if L0 is None: # all neurons spiked at t=0 self._L = self.array.array('l',[0]*len(SG_obj)) else: # check L0 if not isinstance(L0,Iterable): raise TypeError('L0 must be an Iterable.') if not len(L0) == len(SG_obj): raise TypeError('L0 length should be ' + str(len(SG_obj)) +'.') if not all([l0 <= 0 for l0 in L0]): raise ValueError('L0 elements should be <= 0.') self._L = self.array.array('l',L0) else: # No need for _L self._L = self.array.array('l',[])
3.13.3.6. <<Network-set-_X-attribute>>
This block sets _X attribute. If X0 is not specified and if a non zero length _X is required by the model, the simplest _X consistent with _L is created. If both L0 and X0 are specified, their consistency is checked.
if self._past_len > 0: if X0 is None: # X0 is not provided if ND_obj.r_max == 1: # all neurons spiked at t=0 self._X = tuple([self.array.array('B',[0]*(self._past_len)+[1]) for i in range(len(SG_obj))]) else: # neurons spiked at time consistent with _L self._X = tuple([self.array.array('B',[0]*(self._past_len+1)) for i in range(len(SG_obj))]) for n_idx in range(len(SG_obj)): last_time = self._L[n_idx] if last_time >= -self._past_len: self._X[n_idx][self._past_len+last_time] = 1 else: # X0 is provided self._X = tuple([self.array.array('B',[0]*(self._past_len+1)) for i in range(len(SG_obj))]) if not isinstance(X0,Iterable): raise TypeError('X0 must be an Iterable.') if not len(X0) == len(SG_obj): raise TypeError('X0 length should be ' + str(len(SG_obj)) +'.') for x_idx in range(len(X0)): if not isinstance(X0[x_idx],Iterable): raise TypeError('X0[' + str(x_idx) + '] should be iterable.') if not len(X0[x_idx]) == self._past_len+1: raise TypeError('X0[' + str(x_idx) + '] length should be ' + str(self._past_len+1) +'.') for past_idx in range(self._past_len+1): if not X0[x_idx][past_idx] in [0,1]: raise ValueError('X0 elements should be binary arrays.') self._X[x_idx][past_idx] = X0[x_idx][past_idx] if ND_obj.r_max > 1: # Make sure _L and _X are consistent for n_idx in range(len(SG_obj)): last_time = self._L[n_idx] msg = 'L0[{0:d}] is not consistent with X0[{0:d}][{1:d}].' if last_time >= -self._past_len: if not self._X[n_idx][self._past_len+last_time] == 1: raise ValueError(msg.format(n_idx,self._past_len+last_time)) else: for t_idx in range(self._past_len,self._past_len+last_time,-1): if self._X[n_idx][t_idx] == 1: raise ValueError(msg.format(n_idx,t_idx)) else: self._X = tuple([])
3.13.4. <<Network-spike-prob>>
Method spike_prob returns the spiking probability of each neuron of the network as a list. The property decorator makes it callable with obj.spike_prob.
@property def spike_prob(self): """Spiking probability of each neuron of the Network.""" return [self.phi(self[i].kind)(self._V[i]) for i in range(len(self))]
3.13.5. <<Network-update_nl_simple>>
This block defines the simplest update method for the non-leakage case without refractory period and without synaptic delay corresponding to Eq. \eqref{eq:simple-discrete-V-evolution}:
def update_nl_simple(self,spike_or_not): """Update Network state depending on Boolean vector 'spike_or_not' for the simplest model: no leakge, no refractory period, no delay.""" self._t_now += 1 #breakpoint() for n_idx in range(len(self)): if spike_or_not[n_idx]: # neuron n_idx spiked self._V[n_idx] = 0 else: # neuron n_idx did not spike for pre in self[n_idx]: if spike_or_not[pre[0]]: # neuron pre[0] spiked self._V[n_idx] += pre[1]
3.13.6. <<Network-update>>
def update(self,spike_or_not): """Update Network state depending on Boolean vector 'spike_or_not'.""" self._t_now += 1 # deal with self._V if len(self._X) > 0: for n_idx in len(self): self._X[n_idx].pop(0) if spike_or_not[n_idx]: self._X[n_idx].append(1) else: self._X[n_idx].append(0) if len(self._L) > 0: for n_idx in len(self): if spike_or_not[n_idx]: self._L[n_idx] = self._t_now
3.13.7. Tests
ntw2 = Network(sg3, dynRef2, V0 = [0.25,0.5,0.75], L0 = [-1,-5,0], X0 = [[0,0,1,0],[0,0,0,0],[0,0,0,1]]) ntw2.spike_prob ntw2.update_nl_simple([True,False,True]) ntw2[1][0] ntw2[1][1]